2arcsin+2arccos

Construct an isosceles triangle $\triangle ABC$ .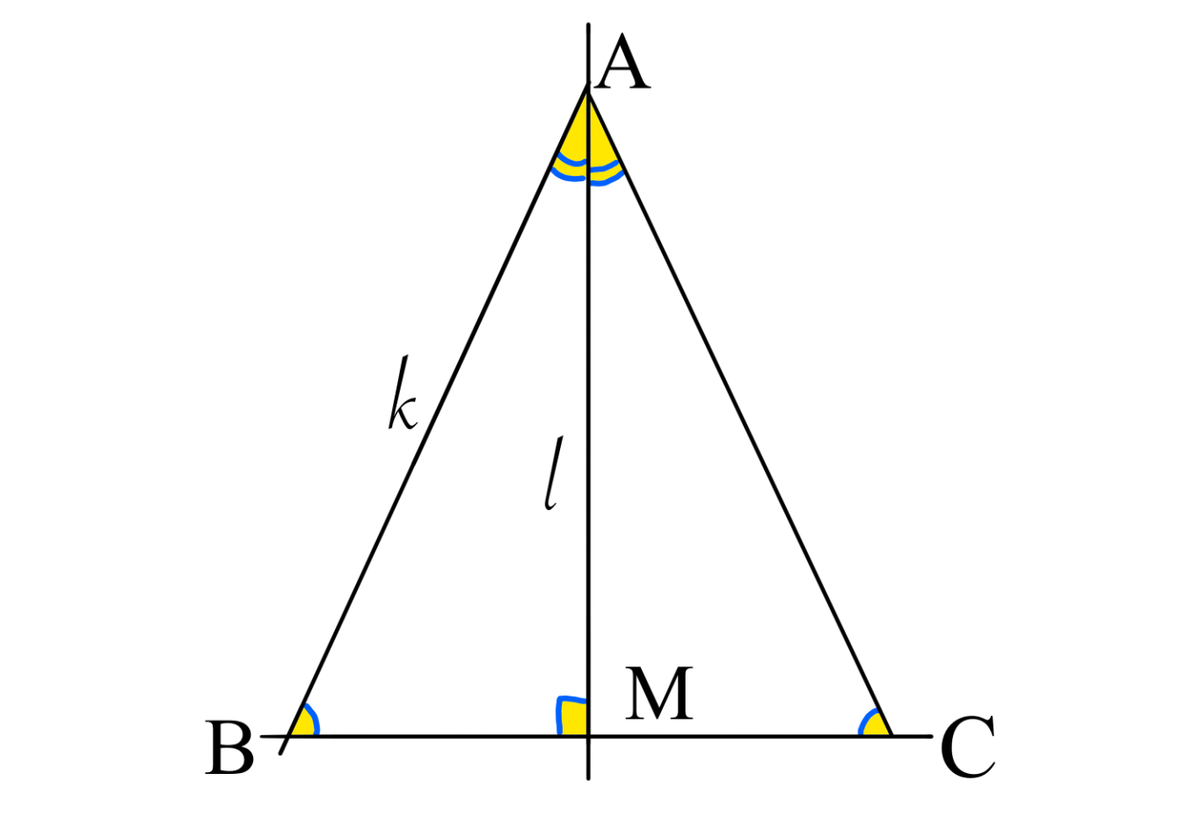
In isosceles $\triangle ABC$ , $BC$ is the base. Construct the median $AM$ where $M$ is the midpoint of $BC$ .

Since $\triangle ABC$ is isosceles, $\angle AMB$ is a right angle.
$\Rightarrow \triangle AMB$ is a right angled triangle.
This part uses basic definitions of sin & cos .
Call the length of the hypotenuse of $Rt\triangle AMB$ $k$ . Call the length of median $AM$ $l$ .
$\Rightarrow \angle BAM=\cos^{-1} \frac{l}{k}.$
$\Rightarrow \angle BAC=2\angle BAM=2\cos^{-1} \frac{l}{k}.$
Since $\triangle AMB$ is right angled, and $\triangle ABC$ is isosceles,
$\sin \angle B=\sin \angle C=\frac{l}{k}.$
$\Rightarrow \angle B=\angle C=\sin^{-1} \frac{l}{k}.$
Let $\frac{l}{k}=n.$ Finally, since $\angle A,\angle B,\angle C$ are the interior angles of a triangle, i.e. they add up to $\pi (rad)$ , $2\cos^{-1} n+2 \times \sin^{-1} n=\pi$ in radians.

Let's use the Mean Function Value Formula from calculus here.:

$\frac{1}{b-a} \cdot \int_{a}^{b} f(x) dx$

Let $f(x) = 2\arcsin(x) + 2\arccos(x)$ over the interval $[-1,1]$ . We now compute:

$\frac{1}{1-(-1)} \cdot \int_{-1}^{1} 2\arcsin(x) + 2\arccos(x) dx;$

or $\frac{1}{2} \cdot 2[\sqrt{1-x^2} + x\arcsin(x) + x\arccos(x) - \sqrt{1-x^2}]|_{-1}^{1};$

or $\arcsin(1) + \arccos(1) + \arcsin(-1) + \arccos(-1) = \frac{\pi}{2} + 0 -\frac{\pi}{2} + \pi = \boxed{\pi}.;$