3-4-5 Square
The diagram above illustrates a square divided into four different-colored triangles, three of them with numbers given as their respective areas.
What is the area of the whole square?
If your result can be expressed in the form a ( b + c d ) , where a , b , c , d are all positive integers, g cd ( b , c ) = 1 , and d is square-free, input a + b + c + d as your answer.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
14 cannot be the area of square
Log in to reply
14 is not the area of the square! The area of the square is A = 4 (3 + 1 x SQUROOT 6), and the digits 4, 3, 1 and 6 add up to 14, Respectfully yours, David
I agree....14 does not seem correct.... I thought maybe 19
Log in to reply
Hehe. How did you get that? :)
maybe provide a solution so we could see it ourselves :)
area=k^2=12+4xsqrt(6)=12+4x2.45=21.8
Let X be the side of the square. Triangle with area of 3... X 6/X 0.5=3 So short side is 6/X Equaly for triangle 4, short side is 8/X For triangle 5... 0.5(X-6/X)(X-8/X)=5 X⁴-24X²+48=0 Let A be the area of the square, A=X² Α²−24A+48=0 A=½(24±√24²−4*48) A=21.79 –
Your solution is fine as it is! The point of skipping all the algebra is to avoid the tedious-reading of the solution. So far, you have done very well! :)
Let X be the side of the square. Triangle with area of 3... X 6/X 0.5=3 So short side is 6/X Equaly for triangle 4, short side is 8/X For triangle 5 0.5(X-6/X)(X-8/X)=5 X⁴-24X²+48=0 Let A be the area of the square, A=X² Α²−24A+48=0 A=½(24±√24²−4*48) A=21.79
Let X be the side of the square. Triangle with area of 3... X6/X0.5=3 So short side is 6/X Equaly for triangle 4, short side is 8/X For triangle 5 0.5(X-6/X)(X-8/X)=5 X⁴-24X²+48=0 Let A be the area of the square, A=X² Α²−24A+48=0 A=½(24±√24²−4*48) A=21.79 –
Let the side of the square be 'l'. Then the other side of the triangle with area 4 must be (8 / l) , (since l x (8 / l) / 2 = 4 which is given). Similarly the other side of the triangle with area 3 must be (6 / l), (since l x (6 / l) / 2 = 3 which is given. And the area of the 3rd triangle with a given area is half of the sides multiplied together, and this area is given as 5. So (l - 8 / l) x (l - 6 / l) / 2 = 5. Multiply both sides of this equation by 2 x l^2 (one l multiplying one bracket, and the other l multiplying the other bracket. So (l^2 - 8) x (l^2 - 6) = 10 x l^2. Now note that the area of the square which I'll call A is equal to l^2. So substituting is gives (A - 8) x (A - 6) = 10 x A. Multiplying and simplifying this equation gives A^2 - 24 x A + 48 = 0. From this A = [24 (+/-) SQUROOT (24^2 - 4 x 1 x 48)] / (2 x 1). So A = 12 (+/-)SQUROOT (96). So A = 12 (+/-) 4 x SQUROOT 6. So A = 4 x [3 (+/-) SQUROOT 6]. Now SQUROOT 6 is clearly more than 2. So the negative value of this root gives A < 4 x [3 - 2]. So for the negative value of the squroot one gets that A<4. This is clearly absurd, because the areas of the 3 triangles that were given add up to 12. (ALTHOUGH I DON'T KNOW WHY THIS ROOT EXISTS FOR THIS EQUATION - I EXPECTED IT TO BE NEGATIVE. CAN SOMEONE EXPLAIN THIS TO ME?). But then the answer is the positive squroot, so the answer is A = 12 + 4 x SQUROOT 6. Which can be expressed as A = 4 x (3 + SQUROOT 6). AND WE'D BETTER NOT FORGET THE ONE TIMES THE SQUROOT!! So A = 4 x (3 + 1 x SQUROOT 6). And finally 4 + 3 + 1 + 6 = 14 which is the answer of this question. Regards, David
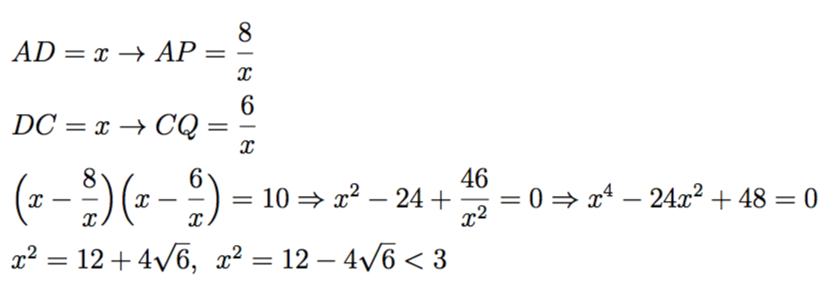
Let k be the side of the square, l the bottom left side, m the bottom right side, n the right bottom side, o the right top side.
Since, it's a square it's true that:
l + m = k and n + o = k
2 1 k l = 4 ⇒ l = k 8
l + m = k ⇒ m = k k 2 − 8
2 1 m n = 5 ⇒ n = k 2 − 8 1 0 k
n + o = k ⇒ o = k 2 − 8 k 3 − 1 8 k
2 1 k o = 3 ⇒ k k 2 − 8 k 3 − 1 8 k = 6 ⇒ k 4 − 2 4 k 2 + 4 8 = 0
The discriminant is:
D = 2 4 2 − 4 ∗ 4 8 = 3 8 4 = 6 4 ∗ 6 ⇒ D = 8 6
k 2 = 2 2 4 ± 8 6 ⇒
k 2 = 1 2 ± 4 6
If we use the negative sign, we see that k 2 = 4 ( 3 − 6 ) ≈ 2 . 2
That can not be the case since k 2 is the area of the square which can not be less than 3.
Therefor:
k 2 = 1 2 + 4 6 ⇒
k 2 = 4 ( 3 + 6 )
So:
a = 4 b = 3 c = 1 d = 6
And the answer is 1 4
Note: Sorry that i've skipped over some tedious algebra