3 arcs

Calculus Level 3

Three quarter-circle arcs enclose an area as shown.

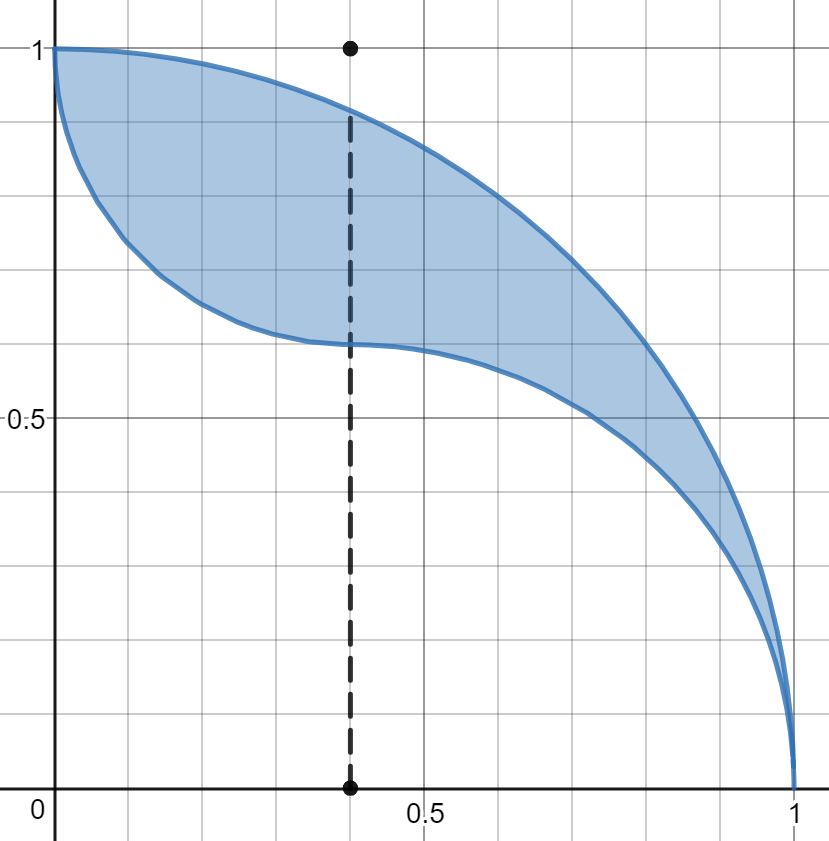
The largest is part of a unit circle, the smaller two are of a size that varies by a parameter $a$ . The vertical line is $x=a$ . The arc to the left of this line has radius $a$ and to the right radius $1-a$ .

The area of the figure is smallest when $a=0$ and largest when $a=1$ .

When $a$ is increased at a constant rate from $0$ to $1$ , when does the area increase most quickly?

Only when

a=0

Always constant Only when

a=0.5

Only when

a=1

Only when

a=0

a=1

2 solutions

Jeremy Galvagni
Oct 28, 2018

The shape is the sum of two arcs less a third. All the arcs are similar so their areas are in proportion to $1^{2}$ , $a^{2}$ , and $(1-a)^{2}$

$1+a^{2}-{1-a}^2=2a$ so the area increases linearly with $a$ . In other words it is $\boxed{\text{Always constant}}$

You can play with the picture via this link: https://www.desmos.com/calculator/pw7c298i0s

Nice analysis, (and desmos graphics), I find that the area $A = \left(\dfrac{\pi}{2} - 1\right) a$ .

Brian Charlesworth - 2 years, 7 months ago

Parth Sankhe
Oct 29, 2018

We can write the area of the figure as

$A=¼π(1)^2 - ¼π(1-a)^2-a(1-a)-(a^2-¼πa^2)$

Differentiating this with respect to time will give us $\frac {dA}{dt}=½π(\frac {da}{dt})$ .

Thus, the rate of change of area is always constant.

3 arcs

2 solutions

0 pending reports