3 - Area

By letting x and y equal those lengths, the area of the rectangle is $4xy=640\text{ cm}^{2}$ (since B and F are midpoints). So $xy=160\text{ cm}^{2}$

Area of triangle ABF = $\frac{xy}{2} = 80\text{ cm}^{2}$

Area of triangle BCD = $xy = 160\text{ cm}^{2}$

Area of triangle DEF = $xy = 160\text{ cm}^{2}$

Subtracting these areas from the orignal rectangle, we get $640\text{ cm}^{2}-80\text{ cm}^{2}-160\text{ cm}^{2}-160\text{ cm}^{2}=\boxed{240\text{ cm}^{2}}$

Triangle BCD is 1/4th the total area. Triangle FDE is also 1/4th the total area. Triangle ABF is 1/8th the total area. This adds to 5/8th, multiply by the total area of 640 $\text{ cm}^2$ to get an area of 400 $\text{ cm}^2$ outside of the triangle. Subtraction reveals that triangle BDF has to be 240 $\text{ cm}^2$ . $\square$

Let's first define some variables. Since opposite sides of a rectangle are congruent, we let AF = FE = x, AB = BC = y . Thus, CD = 2x and ED = 2y . Given that the area of the entire rectangle is 640 $\text{ cm}^2$ [we will leave off the units for the sake of writing a clear explanation and return them when we have a final solution] and the area of a rectangle is found by multiplying the base and the height, we can set up the equation CD * ED = 2x * 2y = 640 which simplifies to 4xy = 640 . If we simplify this equation, by dividing 4 on both sides of the equation, we obtain xy = 160 .

Using this we can find the areas of triangles ABF , BCD , and DEF using the formula .5 * base * height and the fact that these are right triangles whose legs are the base and the height. Thus, the area of triangle ABF is A(ABF) = .5 * xy = .5 * 160 = 80 , the area of triangle BCD is A(BCD) = .5 * y * 2x = xy = 160 , and the area of triangle DEF is A(DEF) = .5 * 2y * x = xy = 160 .

Now that we have found the areas of the triangles, we can use these areas and the area of the rectangle to find the area of triangle BDF Thus subtracting the areas of the triangles from the area of the rectangle, A(BDF) = A(ABCDEF) - A(ABF) - A(BCD) - A(DEF) = 640 - 80 - 160 - 160 = 240 . Therefore, the area of triangle BDF is 240 $\text{ cm}^2 .\square$

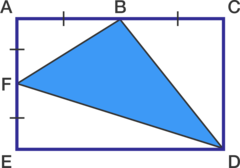The rectangle

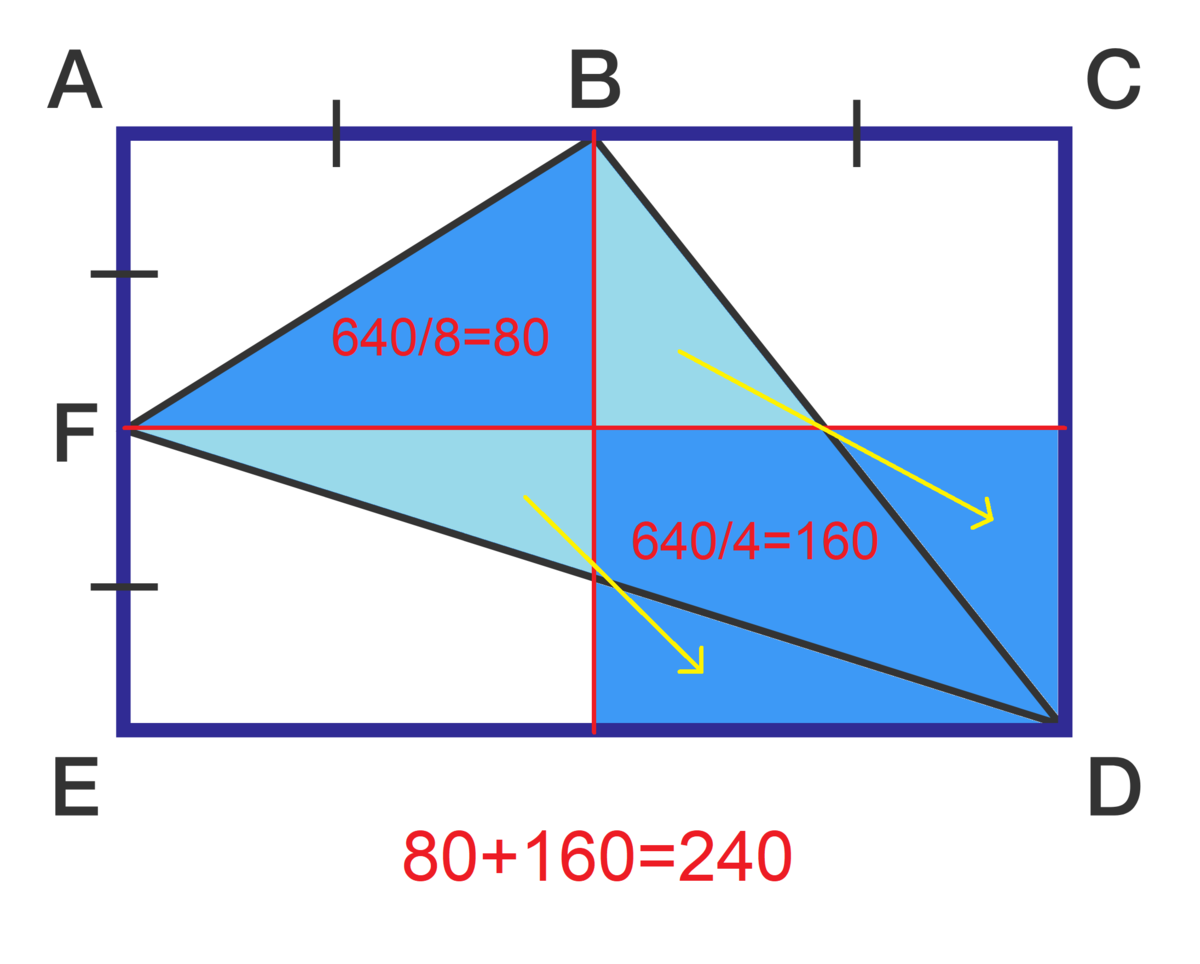
Call the area of the rectangle $\color{#D61F06}A$ .

• Draw a line that bisects the rectangle into left-right halves.

• Draw a line that bisects the rectangle into top-bottom halves.

• It is seen that the upper left triangle is one-half of the upper-left quadrant, or $\color{#D61F06} \frac{1}{8}A$ .

• It is seen that the lower triangle is one-half the bottom half of the rectangle, or $\color{#D61F06} \frac{1}{4}A$ .
• It is also seen that the triangle on the right is one-half the right half of the triangle, or $\color{#D61F06} \frac{1}{4}A$ .

The three triangles make up $\color{#D61F06} \frac{1}{8}A + \frac{1}{4}A + \frac{1}{4} A = \frac{5}{8}A$ .

$\color{#D61F06}\therefore$ the $\color{#3D99F6}{blue}$ triangle's area is $\color{#D61F06}1 - \frac{5}{8} = \frac{3}{8}A$ .

The area of the $\color{#3D99F6}{blue}$ triangle is $\color{#D61F06} \frac{3}{8} \times 640 cm^2 = \boxed{240 cm^2}$

Assume sides of ractangle as 16 and 40 Than 640-(area of ∆abf+∆bcd+∆def) =640-((20.8/2) +( 20.16/2 )+ (40.8/2)) =640-400 =240 Answer

Do not be fooled. Just remember that a square is also a rectangle. This immediately let you know that the sides are 80 and each half side is 40. This lets you calculate the area of the three triangles

area of triangle bcd plus area of triangle FED equal half the area of the rectangle and are of the triangle ABF equal 1/8 area of rectangle so area of triangle FBD equal 640-640/2-640/8 = 240

AE AC=640, LET AC=80CM, therefore, 80AE = 640, solving for AE = 8cm then AF=4cm and AB=40cm. triangle BFD=area of rectangle ACDE- area of triangles (ABF+FED+BCD) . Aabf=1/2(4 40)=80cm Afed=1/2(80 4)=160cm ABCD=1/2(8 40)=160cm therefore area of triangles (ABF+FED+BCD)=80+160+160=400CM2 FINALLY area of BFD=640-400=240cm2

This problem reads "The points B and F are midpoints of the sides BC and AE, " Correct me if I am wrong but should it not be side AC and AE that B and F are the midpoints of?