3-D Analytic Geometry
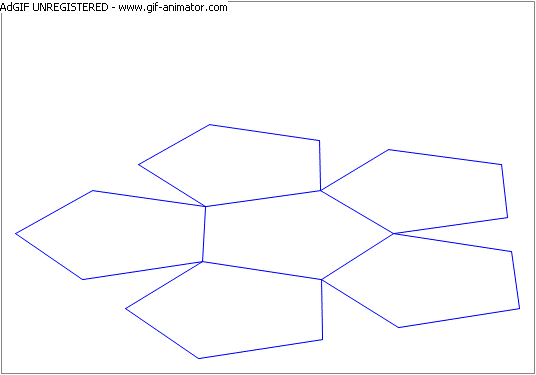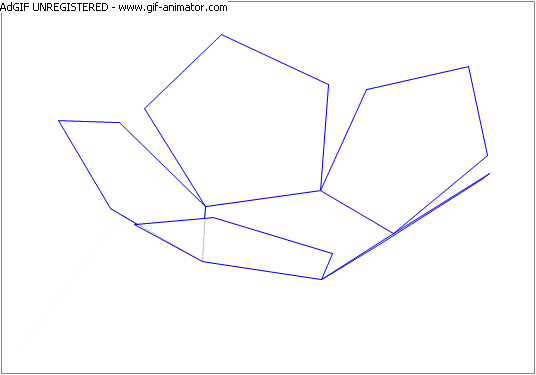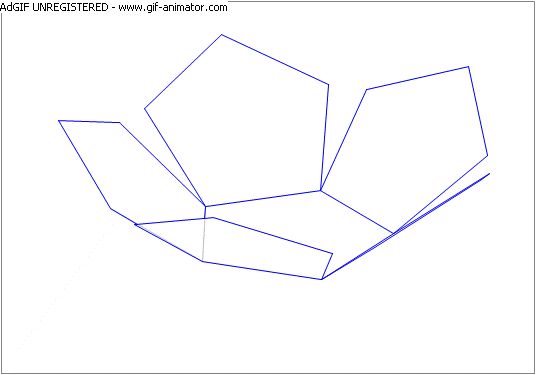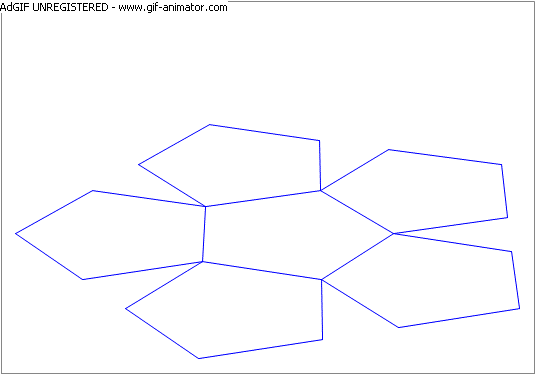 Five regular pentagons are placed symmetrically around a central pentagon of the same size, as shown in the attached figure. The five pentagons are then rotated about the common side each has with the central pentagon. By what angle (in degrees) is each pentagon rotated so that the five pentagons join sides at the end of the rotation?
Five regular pentagons are placed symmetrically around a central pentagon of the same size, as shown in the attached figure. The five pentagons are then rotated about the common side each has with the central pentagon. By what angle (in degrees) is each pentagon rotated so that the five pentagons join sides at the end of the rotation?
- See the attached animation.
- Give your answer to three decimal places.
The answer is 63.435.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I also did the same
58.2825 d can be calculated as
ASin [Sqrt(1- 2 Sin 18 d)/ Tan 36 d] Or just
ASin [1/ Sqrt(2 - 2 Sin 18 d)] Or ATan[0.5 (1 + Sqrt(5))]
i.e. 58.282525588538994675786096860227 d.
ASin (2 Cos 36 d/ Sqrt(3)) + ASin (1/ (Sqrt(3) Tan 36 d)) being minus by 180 d; angle wanted should be obtained by intersection of two planes, each formed by at least 3 different points in 3 D space.
180 d - 2 (58.2825 d ) = 63.435 d is true as 180 d - 2 ATan [0.5 (1 + Sqrt(5))] = ATan (2); our proof should not be just like this.
These are trigonometry rather than geometry. Turn to geometry,
Plane of (-1, 0, 0), (1, 0, 0) and (0, 1/ Sqrt(3), Sqrt[Sqr(Tan 36 d) - 1/3]) intersects with plane of (0, Sqrt(3), 0), (1, 0, 0) and (0, 1/ Sqrt(3), Sqrt[Sqr(Tan 36 d) - 1/3]) produces the wanted angle of 63.435 d when the acute angle is chosen. Total of 4 different points in space for an angle.
The mentioned 'Geometry' seems to deny for ability to apply only trigonometry for the answer.
With h = Sqrt[Sqr(Tan 36 d) - 1/3],
0 x + 2 h y - 2/ Sqrt(3) z + 0 = 0 and
Sqrt(3) h x + h y + (Sqrt(3) - 1/ Sqrt(3)) z - Sqrt(3) h = 0
Cos Q = | (2 h^2 - 4/ 3)/(4 h^2 + 4/ 3) | = 1/ (Cosec 18 d - 1)
= 0.44721359549995793928183473374626 {Exact}
= 1/ Sqrt(5)
Q = 63.434948822922010648427806279547 d {Exact}
= ATan(2)
Online calculator:
http://onlinemschool.com/math/assistance/cartesiancoordinate/plane/ http://onlinemschool.com/math/assistance/cartesiancoordinate/plane_angl/
Approximations:
-0.882112 y + 1.154701 z = 0 and {Same with equation multiplied by -1, for better entries.}
0.7639314 x + 0.4410564 y + 1.154701 z - 0.763931 = 0
Cos Q = 0.4472142382745872 {Not exact}
Q = 63.434907647653166057024958592001 d {Not exact}
{For easier reading and introduction to availability.}
Cos Q = |a1 a2 + b1 b2 + c1 c2|/ Sqrt[(a1 a1 + b1 b1 + c1 c1)(a2 a2 + b2 b2 + c2 c2)] for 3 dimensional planes of a1 x + b1 y + c1 z + d1 = 0 intersects with a2 x + b2 y + c2 z + d2 = 0.
Sec(180 d/ 3) = 2; Sec(180 d/ 4) = Sqrt(2) while Sec(180 d/ 5) met with another type of irrational numbers for special studies.
8 s^5 - 4 s^4 - 6 s^3 + 6 s^2 + 2 s - 1 = 0
s1 = 0.309016994374947 = Sin (18 d)
s2 = -0.809016994374948 = - Cos (36 d)
s3 = -0.565197717383639
s4 = 0.782598858691820 + j 0.521713717946516
s5 = 0.782598858691820 - j 0.521713717946516
S^2 +/- 2 (¼) S - ¼ = 0:
s = Sin 18 d = [Sqrt(5) - 1)]/ 4 = 0.30901699437494742410229341718282
C = Cos 36 d = [Sqrt(5) + 1)]/ 4 = 0.80901699437494742410229341718282
8 s^5 - 4 s^4 - 6 s^3 + 6 s^2 + 2 s - 1 = 0
8 C^5 + 4 C^4 - 6 C^3 - 6 C^2 + 2 C + 1 = 0
4 C^5 - 6 C^4 + 13 C^3 - 9 C^2 - C + 1 = 0
4 s^5 + 6 s^4 + 13 s^3 + 9 s^2 - s - 1 = 0
4 S^2 +/- 2 S - 1 is their common factor. These explained Tan^2 (36 d) = 2 [1 - 3 Sin (18 d) + 2 Sin^2 (18 d)].
I call these the pentagonal polynomials.
x^4 + x^3 + x^2 + x + 1 = 0
x^4 - x^3 + x^2 - x + 1 = 0
For their existence to be met.
Sin P = Sqrt[½ + Sqrt(5)/ 10] = 0.85065080835203993218154049706301
P = 58.282525588538994675786096860227 d
Cos Q = 1/ Sqrt(5) = 0.44721359549995793928183473374626
Q = 63.434948822922010648427806279547 d
Surd forms are obtainable from clue of pentagonal polynomials as Sin 18 d and Cos 36 d forming quadratic equation S^2 +/- 2 (¼) S – ¼ = 0. Every angle can be converted into arc tangent.
Tan P = [1 + Sqrt(5)]/ 2 and Tan Q = 2.
Tan 2 P = 2 Tan P/ [1 – (Tan p)^2] = [1 + Sqrt(5)]/ [1 – 3/ 2 - Sqrt(5)/ 2] = 2 [1 + Sqrt(5)]/ [2 – 3 - Sqrt(5)] = -2 [1 + Sqrt(5)]/ [1 + Sqrt(5)] = -2.
Pi – Q = 2 P as
Tan (Pi – Q) = -Tan Q = - 2 while Tan 2 P = -2
=> - Tan Q = Tan 2 P = - 2 i.e. Q = ATan 2.
P = ATan [0.5 (1 + Sqrt (5))] = 58.282525588538994675786096860227 d
Q = ATan 2 = 63.434948822922010648427806279547 d
Same here!
Exactly as I did!!
Consider the orthogonal projection of the 5 pentagons onto the XY plane, after the rotation. At this point, the line segments joining the vertices that unite, at the end of the rotation, form a larger pentagon.
A right triangle (shown in red, in the second image), can be drawn with a hypotenuse (first image, the initial frame) equal to
h = e sin ( 1 0 8 ∘ )
where e is the length of the edge.
Back to the first image, we note that (the black segment) is the apothem a of the pentagon (the perpendicular distance from the center of the pentagon to any of its sides). We have
a = e / ( 2 tan ( 7 2 ∘ / 2 ) ) = e / ( 2 tan ( 3 6 ∘ ) )
Now considering the larger pentagon, it edge length is given by
e ′ = 2 e sin ( 1 0 8 ∘ / 2 ) = 2 e sin ( 5 4 ∘ )
Hence by similarity, the apothem of the larger pentagon is scaled by the same ratio as the edges of the pentagon, and therefore,
r = a ′ / a = e ′ / e = 2 sin ( 5 4 ∘ ) )
When the rotation is complete, the difference between the two apothems is the adjacent side to the sought angle of rotation.
Hence,
x = a ′ − a = a ( a ′ / a − 1 ) = a ( r − 1 )
Finally, we can write,
cos θ = x / h = ( r − 1 ) ( e / ( 2 tan ( 3 6 ∘ ) ) / ( e sin ( 1 0 8 ∘ ) )
cos θ = ( 2 sin ( 5 4 ∘ ) ) − 1 ) / ( 2 sin ( 1 0 8 ∘ ) tan ( 3 6 ∘ ) )
cos θ = 0 . 4 4 7 2 1 3 5 9 5 4 9 9 9
Hence,
θ = 6 3 . 4 3 5 ∘
This can be solved simply in 3 steps by taking components of sides.
Step1: Realize that the edges meet in the plane of symmetry as shown. Let the angle by which pentagon is rotated (the one we have to find) be α. And let the edge make angle β in the plane of symmetry.
 Plane of symmetry
Plane of symmetry
Step2: Refer to the image below. We know the angles 54 and 18. Lengths of parts highlighted in blue should be equal.
 First condition
Hence
First condition
Hence
L cosβ cos54 = L sin18
Or β = 58.16
Step3: The vertical components as shown below should be equal.
 Second condition
Hence
Second condition
Hence
L cos18 sin α = L sin β
Substituting β from step 2,
α = 63.435
@Hosam Hajjir can we generalise this for n-sided polygon? like for squares its 90 degrees, for triangle its 120.
This problem will work for n = 3 , (which will result in a tetrahedron), and n = 4, (resulting in a cube), and n = 5 (which is this problem). However, for n = 6, the hexagons are already joining sides at the initial position (without any rotation). For n > 6, there is no angle of rotation that will result in the polygons joining sides. Thanks for your remark.
I would be easier to explain if I know how to post images here. Help me if you know how.
Let a vertex of the central pentagon on the x-y plane be A. The movable pentagon on the right be ABCDE and the left, AB'C'D'E'. The points are assigned symmetrically at A, so that B and B', C and C', D and D', and E and E' are equidistant from A. So that what is true on ABCDE is also true on AB'C'D'E'. B and B' are the nearest vertices on the movable pentagons to A. BD is parallel to AE and likeswise B'D' and AE'. Let the line from A perpendicular to BD meet BD at F. Now if we look directly on top, when the pentagons rotate up, we note that BD is always parallel to AE, the length BF remains the same, and the projection of AF is always perpendicular to BD and AE. The projection of of AF just get shorter as the angle of rotation increases to 9 0 o . It is the same for B'D', B'F' and AF'. The distance between B and B' becomes shorter as the angle of rotation increases until B and B' coincide.
Let BF = B'F' = a , AF = AF' = b and the angle of rotation be θ . Then the projection of AF, x = b cos θ . Since BD and B'D' are always parallel to AE and AE' respectively. When B and B' coincide, ∠ D B D ′ = ∠ E A E ′ = 1 0 8 o and ∠ A B F = 2 1 ∠ D B D ′ = 5 4 o . It is noted that the projection of AF, x = a tan 5 4 o , Therefore,
⇒ x = b cos θ = a tan 5 4 o
⇒ cos θ = b a tan 5 4 o
We note that ∠ C B D = 2 1 ( 1 8 0 o − ∠ B C D ) = 2 1 ( 1 8 0 o − 1 0 8 o ) = 3 6 o .
Therefore, ∠ D B A = ∠ C B A − ∠ C B D = 1 0 8 o − 3 6 o = 7 2 o and ∠ B A F = 9 0 o − 7 2 o = 1 8 o .
⇒ tan 1 8 o = b a
⇒ cos θ = b a tan 5 4 o = t a n 1 8 o tan 5 4 o = 0 . 3 2 4 9 1 9 6 9 6 × 1 . 3 7 6 3 8 1 9 2 = 0 . 4 4 7 2 1 3 5 9 5
⇒ θ = cos − 1 0 . 4 4 7 2 1 3 5 9 5 = 6 3 . 4 3 5 o
solved by planar line symmetry.
This is half of a regular dodecahedron , so a trip to Wikipedia gives that the dihedral angle (angle between two adjacent sides) is 2 arctan ϕ ≈ 1 1 6 . 5 6 5 ∘ . Thus the pentagons must be rotated by 1 8 0 ∘ − 2 arctan ϕ ≈ 6 3 . 4 3 5 ∘ .