3-D Geometry

Geometry Level 4

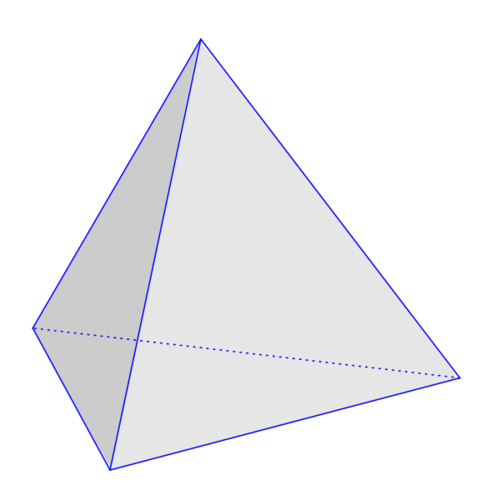A point $P$ inside a regular tetrahedron is such that its distance from all vertices $A, B, C$ & $D$ of the tetrahedron is the same. The line $AP$ , when produced, intersects the plane formed by vertices $B, C$ & $D$ at the point $Q$ . The ratio $\frac{AP}{AQ}$ can be written as $\frac{a}{b}$ .

Find $a^{b}$ .

Try more from my set Geometry Problems .

Image credit: Wikipedia Aldoaldoz

The answer is 81.

1 solution

Caleb Townsend
Feb 5, 2015

Note that $AP$ is the radius of the circumsphere, and $AQ$ is the height of the tetrahedron. Then $\frac{AP}{AQ} = \frac{(\frac{a\sqrt{6}}{4})}{(\frac{a\sqrt{6}}{3})} = \frac{3}{4}$ so $\frac{a}{b} = \frac{3}{4}$ . Assuming the author meant that $\frac{AP}{AQ}$ can be written as $\frac{a}{b}$ where $a$ and $b$ are positive coprime integers, this means $a = 3$ and $b = 4$ . Finally $3^4 = \boxed{81}$

3-D Geometry

Image credit: Wikipedia Aldoaldoz

The answer is 81.

1 solution

0 pending reports