3 in a crowd
Three uniform spheres are mutually tangent to one another and tangent to the hemisphere. The point of tangency between the lower sphere and the hemisphere is the center of the hemisphere. What is the ratio of the radius of the hemisphere to the radius of one of the spheres?
Give the solution with 4 decimal places.
The answer is 3.9093.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
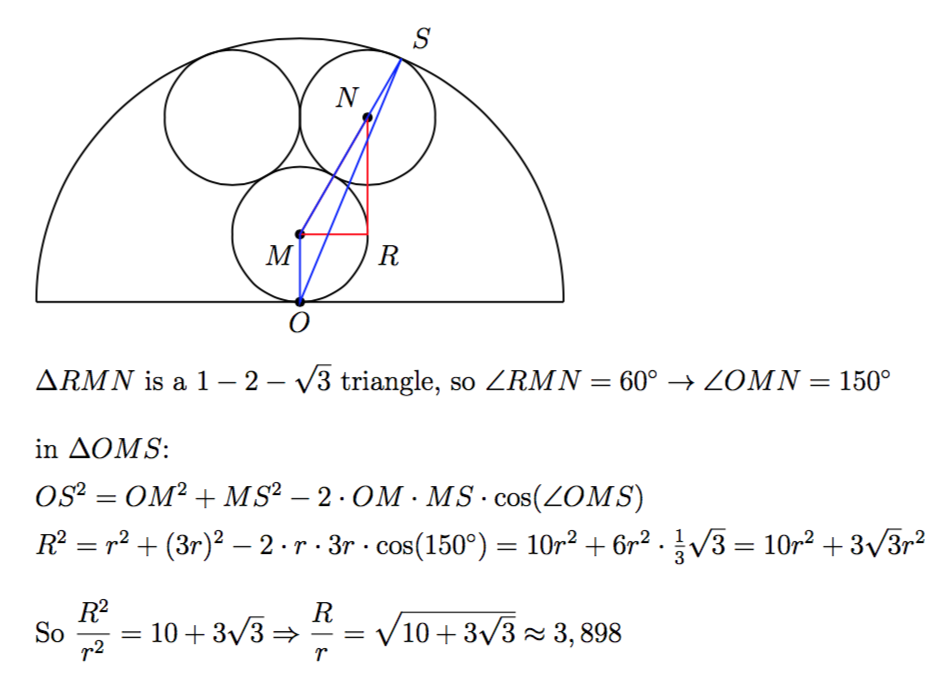
The spheres are touching such that the circles that represent the largest-area cross-section will form a figure like the one shown, and the three dimensional aspect can then be safely ignored.
We can assume without loss of generality the radius of the spheres r = 1 . This means the ratio desired is R / r = R / 1 = R .
As X Y Z is an equilateral triangle and r = 1 , by the properties of a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle m X P = 3 . This implies m O P = 3 + 1 .
Applying the Pythagorean theorem, m O Z must be 1 2 + ( 3 + 1 ) 2 = 1 + 1 + 2 3 + 3 = 5 + 2 3 .
Since R = m O Z + 1 , R = 5 + 2 3 + 1 ≈ 3 . 9 0 3 9 3 .