3 known, 3 unknown
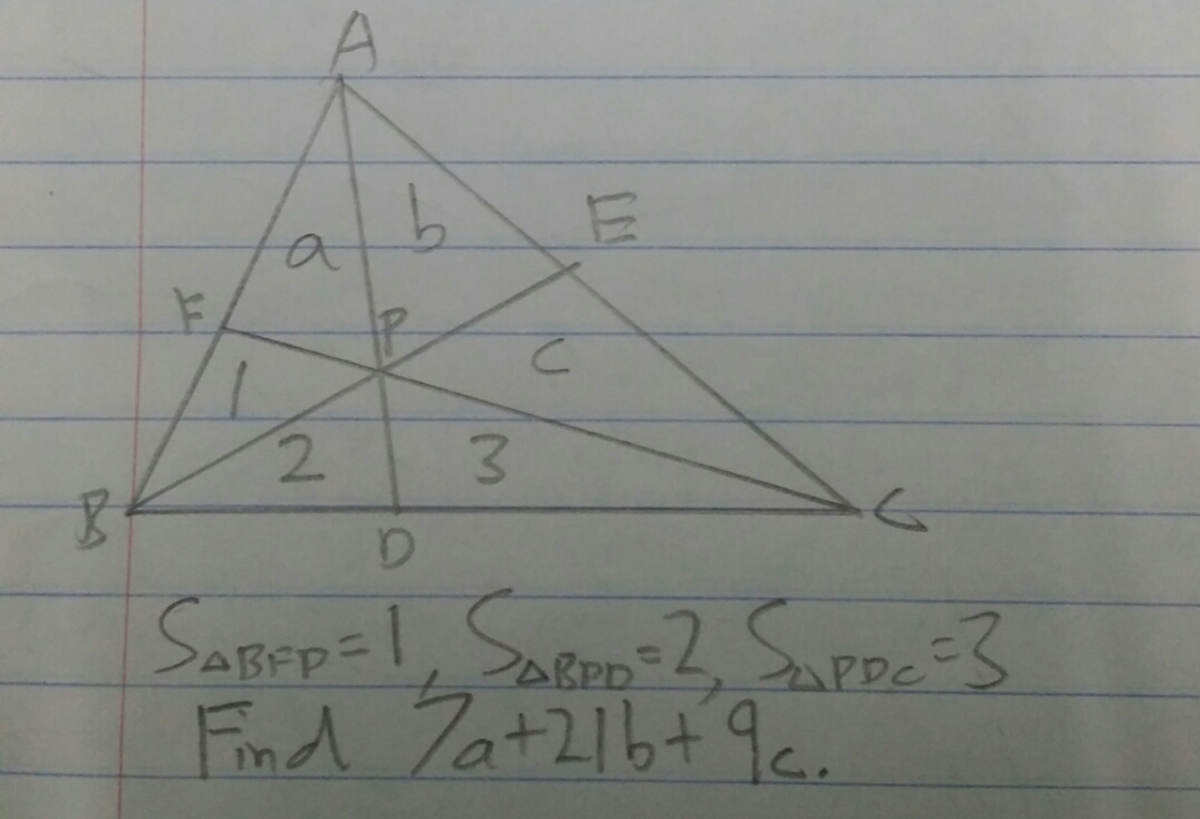
Given a triangle △ A B C and a point P . A P , B P , C P intersect B C , A C , A B at point D , E , F respectively. A r e a △ B P F = 1 A r e a △ B P D = 2 A r e a △ C P D = 3 A r e a △ A P F = a A r e a △ A P E = b A r e a △ C P E = c Find 7 a + 2 1 b + 9 c
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 This solution use the theorem 'ratio of length = ratio area of triangle with same height' frequently (Exp:
F
P
C
F
=
A
r
e
a
△
P
F
B
A
r
e
a
△
C
F
B
). Apply Ceva theorem with
△
B
P
C
and point
A
. We get
D
C
B
D
×
F
P
C
F
×
E
B
P
E
=
1
3
2
×
1
1
+
2
+
3
×
c
+
3
+
2
c
=
1
4
c
=
c
+
5
c
=
3
5
Apply Ceva theorem with
△
A
P
B
and point
C
. We get
F
B
A
F
×
E
P
B
E
×
D
A
P
D
=
1
1
a
×
c
2
+
3
+
c
×
2
+
1
+
a
2
=
1
8
a
=
a
+
3
a
=
7
3
Apply Ceva theorem with
△
A
B
C
and point
P
. We get
F
B
A
F
×
D
C
B
D
×
E
A
C
E
=
1
1
a
×
3
2
×
b
c
=
1
b
=
2
1
1
0
Hence, the answer is
7
a
+
2
1
b
+
9
c
=
2
8
.
This solution use the theorem 'ratio of length = ratio area of triangle with same height' frequently (Exp:
F
P
C
F
=
A
r
e
a
△
P
F
B
A
r
e
a
△
C
F
B
). Apply Ceva theorem with
△
B
P
C
and point
A
. We get
D
C
B
D
×
F
P
C
F
×
E
B
P
E
=
1
3
2
×
1
1
+
2
+
3
×
c
+
3
+
2
c
=
1
4
c
=
c
+
5
c
=
3
5
Apply Ceva theorem with
△
A
P
B
and point
C
. We get
F
B
A
F
×
E
P
B
E
×
D
A
P
D
=
1
1
a
×
c
2
+
3
+
c
×
2
+
1
+
a
2
=
1
8
a
=
a
+
3
a
=
7
3
Apply Ceva theorem with
△
A
B
C
and point
P
. We get
F
B
A
F
×
D
C
B
D
×
E
A
C
E
=
1
1
a
×
3
2
×
b
c
=
1
b
=
2
1
1
0
Hence, the answer is
7
a
+
2
1
b
+
9
c
=
2
8
.
The key idea is that if 2 triangles have the same height then the ratio of their areas is equal to the ratio of there base lengths. [ A C D ] [ A B D ] = C D B D But we also have [ P C D ] [ P B D ] = C D B D
Thus [ A C D ] [ A B D ] = [ P C D ] [ P B D ]
b + c + 3 a + 3 = 3 2
3 a + 3 = 2 b + 2 c
Working similarly with other pairs of triangles gives 5 a = b + c and c + c a = 5 b
Plugging 5 a = b + c into 3 a + 3 = 2 b + 2 c gives a = 3 / 7
From there we can get c = 5 / 3 and b = 1 0 / 2 1