Spin Around The Pin
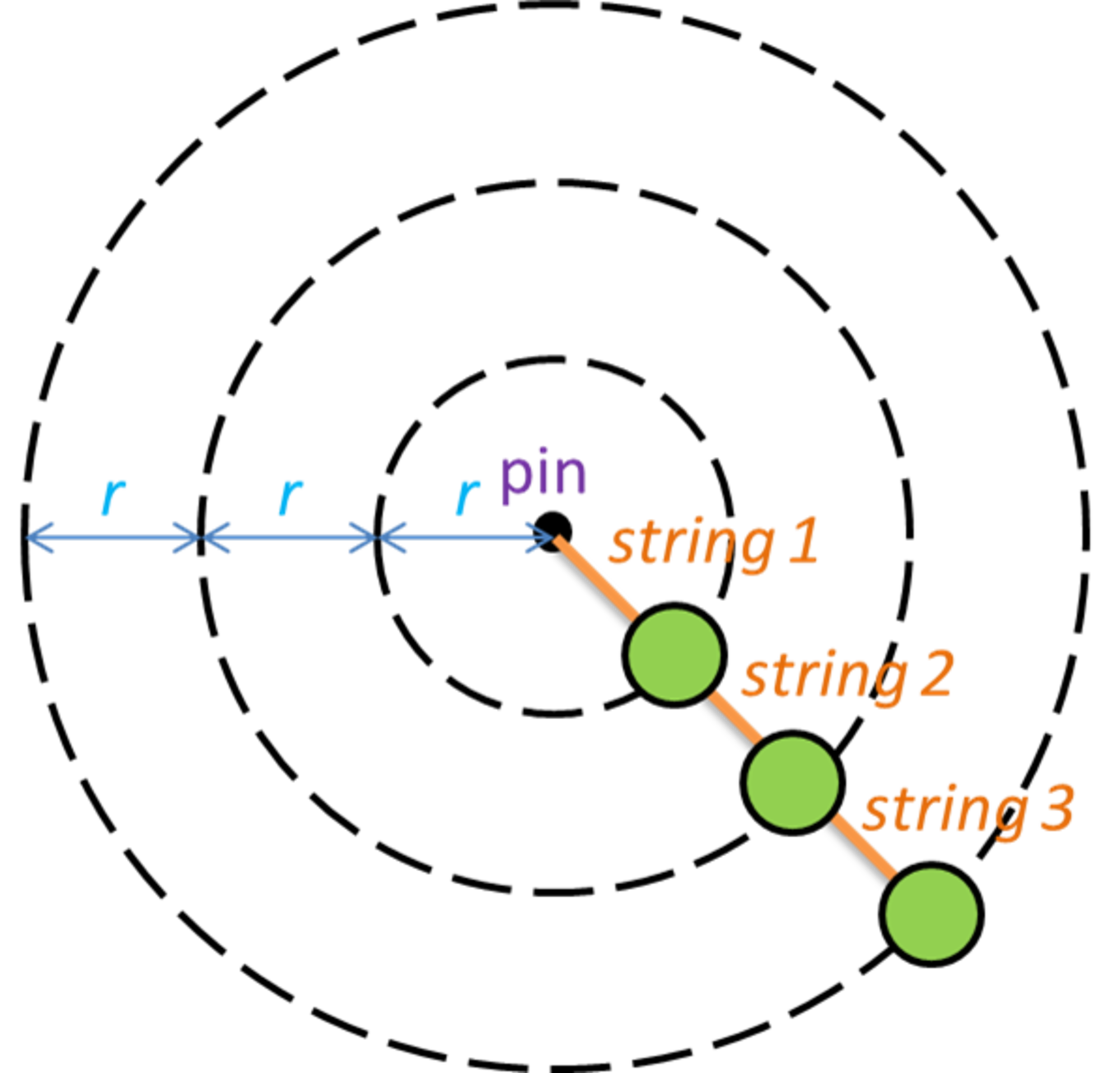
Three identical masses are fixed to a string with even spacing, and spun around a pin in free space. Determine the ratio of the tension in the string before the first mass, to the tension in the string between the first and second mass, to the tension in the string between the second and third mass given that r = 0 . 5 6 m and that the period of rotation is 1 . 1 2 s .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let T 1 , T 2 , and T 3 be the three tension forces in question. Since the system is undergoing uniform circular motion, we know that the net force on each mass j is F j = m ω 2 r j radially inward.
Begin with the outermost mass, which is acted upon by a single force. Applying the above equation yields T 3 = m ω 2 3 r . Moving to the middle mass, we find T 2 − T 3 = m ω 2 2 r T 2 = m ω 2 5 r . Likewise, T 1 − T 2 = m ω 2 r T 1 = m ω 2 6 r . When we take the ratios, we find T 1 : T 2 : T 3 = 6 : 5 : 3 .
The net force of each mass (along the plane of circular motion) contributes to the centripetal force to maintain its circular motion, which is directly proportional to the radius of the mass's uniform circular motion. Therefore, the net force on each mass (from inwards to outwards) is 1:2:3 and the tension in each string can be determined by drawing the above free body diagrams (assuming WLOG that the net force on the outwardmost mass is 3 F N .)