3 on a wire

Geometry Level 5

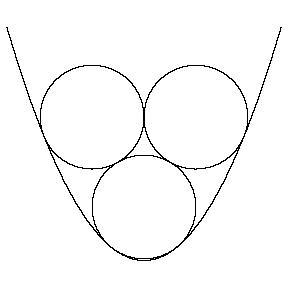
Three uniform circles are externally tangent to one another and internally tangent to the parabola $y = x^{2}$ . Find the magnitude of the radius.

Provide the answer to 5 decimal places.

The answer is 0.64334.

2 solutions

Mark Hennings
Nov 16, 2016

If the radius vector to either of the points of tangency of the bottom circle with the parabola makes angle $\theta$ with the downward vertical, it follows that $2r\sin\theta \; = \; \tan\theta$ If the radius vector to the point of tangency of either of the top two circles makes an angle $\phi$ with the downward vertical, then $2r(1 + \sin\phi) \; = \; \tan\phi$ These two conditions ensure that we have the right gradients at these points of tangency. We also need to ensure that the upper and lower points of tangency are the correct vertical height apart, and so $r^2\big[(1+\sin\phi)^2 - \sin^2\theta\big] \; = \; r\big(\sqrt{3} + \cos\theta - \cos\phi\big)$ so that $r(1+\sin \phi + \sin\theta)(1 + \sin\phi - \sin\theta) \; = \; \sqrt{3} + \cos\theta - \cos\phi$ Solving these three conditions numerically, we deduce that $r = 0.643337...$ , making the answer $\boxed{0.64334}$ .

Wow, that's a very concise solution!

Calvin Lin Staff - 4 years, 7 months ago

Cannot understand even 1 percent.

The concept you have used is very unknown to me. Do you have some coordinate geometry proof?

Priyanshu Mishra - 4 years, 7 months ago

This is a coordinate geometry approach. If the radius vectors to the point of tangency of the bottom circle makes an angle $\theta$ with the downward vertical, then the $x$ -coordinate of the point of tangency is $r\sin\theta$ , and hence the gradient of the parabola at that point is $2r\sin\theta$ . But the gradient of the tangent to the circle at that point is $\tan\theta$ . This gives the first equation. The second equation comes from applying the same argument to the point of tangency of a top circle with the parabola. The third equation comes from comparing the difference in heights between those points of tangency, firstly calculated as points on the parabola (with known $x$ -coordinates), and then calculated as points on the two circles. Try drawing a diagram.

Mark Hennings - 4 years, 7 months ago

An alternative algebraic solution:

Assume the bottom circle is centered at (0,p) and is tangent at (z,z^2), where z is non-negative. The reciprocal of the slope of the normal would then be -2z which, by a slope computation equates to

-z/(p-z^2) = -2z, or z = 2z(p - z^2).

This would mean that either z = 0 or p-z^2 = 1/2. The former occurs when p ≤ 1/2 and the latter when p ≥ 1/2.

Letting r be the radius, we then have when p ≤ 1/2, r = p. If p ≥ 1/2, we have r^2 = (p - z^2)^2 + z^2 = p - 1/4, and so r = sqrt(p - 1/4).

Let the upper right hand circle be centered at (r,s). Then s = p + Sqrt[3] r, by drawing the common radii and calculate using the pythagoras formula. Assume this circle is tangent at (x,x^2). We then obtain the equations

r^2 = (r-x)^2 + (s-x^2)^2 from distances, and (s-x^2)/(r-x) = -1/2x from the slope of the normal.

Derive the following equations for r and s in terms of x.

s = x sqrt(4x^2 + 1) - x^2 and r = 4x^3 - 2x^2 sqrt(4x^2+1) + x

If p ≥ 1/2, then r = sqrt(p - 1/4), s = p + Sqrt(3) r, solve the two equations with two unknowns and find x = 1.240 and r = 0.64334 (and p ≥ 1/2 is satisfied)

Assuming p ≤ 1/2, we'd have r = p, s = (1+Sqrt(3)) p, and x = 1.222, r = 0.63473 which does not meet: p ≤ 1/2. Meaning there is no solution for p ≤ 1/2.

W Rose - 4 years, 7 months ago

Can you post this as a seperate solution? Thanks!

Calvin Lin Staff - 4 years, 6 months ago

W Rose
Nov 18, 2016

Assume the bottom circle is centered at (0,p) and is tangent at (z,z^2), where z is non-negative. The reciprocal of the slope of the normal would then be -2z which, by a slope computation equates to ...

-z/(p-z^2) = -2z, or
z = 2z(p - z^2).

This would mean that either z = 0 or p-z^2 = 1/2. The former occurs when p ≤ 1/2 and the latter when p ≥ 1/2.

Letting r be the radius, we then have when p ≤ 1/2, r = p. If p ≥ 1/2, we have r^2 = (p - z^2)^2 + z^2 = p - 1/4, and so r = sqrt(p - 1/4).

r^2 = (r-x)^2 + (s-x^2)^2 from distances, and
(s-x^2)/(r-x) = -1/2x from the slope of the normal.

Derive the following equations for r and s in terms of x.

s = x sqrt(4x^2 + 1) - x^2 
r = 4x^3 - 2x^2 sqrt(4x^2+1) + x

If p ≥ 1/2, then r = sqrt(p - 1/4), s = p + Sqrt(3) r, solve the two equations with two unknowns and find x = 1.240 and r = 0.64334 (and p ≥ 1/2 is satisfied).

Assuming p ≤ 1/2, we'd have r = p, s = (1+ Sqrt(3)) p, and x = 1.222, r = 0.63473 which does not meet p ≤ 1/2. Meaning there is no solution when p ≤ 1/2.

3 on a wire

The answer is 0.64334.

2 solutions

0 pending reports