3 points on a straight line!

Geometry Level 3

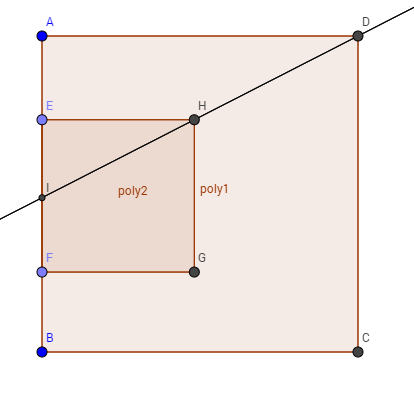
The above shows two squares A B C D ABCD and E F G H EFGH with side lengths 10 and 6, respectively. Given that A , E , F A,E,F and B B lies on a straight line. And the straight line A E AE has a distance of 1.

If A I ⃗ = β E I ⃗ \vec{AI} = \beta \vec{EI} , what is the value of β \beta ?

3 5 \frac{3}{5} 1 2 \frac{1}{2} 5 3 \frac{5}{3} 2 3 \frac{2}{3}

Omar Sehlouli by Omar Sehlouli , 21, Morocco

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hana Wehbi
May 20, 2016

Triangles A D I a n d E H I ADI and\ EHI are similar triangles by A.A.A.

∠ I = ∠ I \angle I= \angle I Reflexive angle.

∠ D = ∠ H \angle D=\angle H Corresponding angles of parallel lines

∠ A = ∠ E \angle A=\angle E = 9 0 d e g 90 ^ {deg} Corresponding angles of parallel lines.

By taking the ratio of proptionality A I E I \frac{AI}{EI} = 10 6 \frac{10}{6} = 5 3 \frac{5}{3}

Keeping in mind two perpendiculars to the same line are parallel.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Great , note that A I E I = A D E H = D H D I = 5 3 \frac{AI}{EI} = \frac{AD}{EH} = \frac{DH}{DI} = \frac{5}{3}

Omar Sehlouli - 5 years ago

Log in to reply

You are right too.

Hana Wehbi - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...