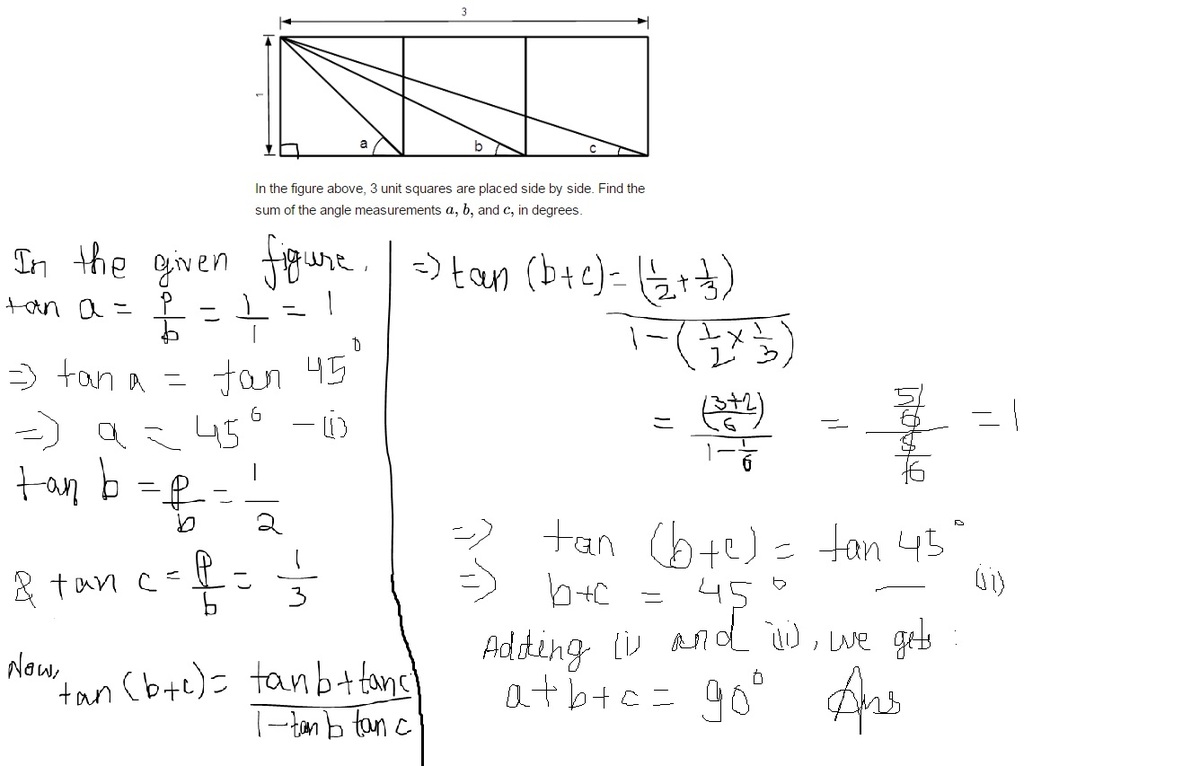
3 Squares Puzzle

2x3 Solution

Since scaling, translating, reflecting, and rotating do not change the triangles' angles, we can reorganize them like so. The sum of the angles becomes trivial.

Note: I scaled the right triangles with angle $a, b,$ and $c$ by $2, \sqrt{2},$ and $1$ respectively.

$(i+1)\cdot (i+2) \cdot (i+3) = 10i$ which has angle $\boxed{90}$ .

On an $xy$ -grid, draw triangle $\Delta ABC$ with coordinates $A(0,3), B(2,2)$ and $C(1,0)$ . Also label the origin $O(0,0)$ and the point $D(3,3)$ .

Then since $AB = BC = \sqrt{5}$ and $AC = \sqrt{10}$ we have that $\Delta ABC$ is a right isosceles triangle, and so $\angle BAC = 45^{\circ}$ , which is also the same value as $a$ .

Now $\angle OAC = c$ and $\angle BAD = b$ . But $\angle OAC + \angle BAC + \angle BAD = 90^{\circ}$ , so $a + b + c = \boxed{90^{\circ}}$ .

Comment: Note that this can be written as

$\arctan(1) + \arctan(\frac{1}{2}) + \arctan(\frac{1}{3}) = \frac{\pi}{2}$ .

Now for $x \gt 0$ we have that $\arctan(\frac{1}{x}) = \frac{\pi}{2} - \arctan(x)$ , (proof below).

So upon substitution we have that

$(\frac{\pi}{2} - \arctan(1)) + (\frac{\pi}{2} - \arctan(2)) + (\frac{\pi}{2} - \arctan(3)) = \frac{\pi}{2}$

$\Longrightarrow \arctan(1) + \arctan(2) + \arctan(3) = \pi$ ,

which is kind of cool. :)

Proof: Let $f(x) = \arctan(x) + \arctan(\frac{1}{x})$ for $x \gt 0$ .

Then $f'(x) = \frac{1}{1 + x^{2}} + (\frac{1}{1 + \frac{1}{x^{2}}})*(-\frac{1}{x^{2}}) = \frac{1}{1 + x^{2}} - \frac{1}{1 + x^{2}} = 0$ .

Thus $f(x)$ must equal some constant for $x \gt 0$ . So plug in any positive value for $x$ to find out what this constant is. We have $f(1) = \frac{\pi}{4} + \frac{\pi}{4} = \frac{\pi}{2}$ , and so $\arctan(\frac{1}{x}) = \frac{\pi}{2} - \arctan(x)$ for $x \gt 0$ .

(Note that for $x \lt 0$ we would have $f(x) = -\frac{\pi}{2}$ , so the formula for $x \lt 0$ would be $\arctan(\frac{1}{x}) = -\frac{\pi}{2} - \arctan(x)$ .)

tan -1 x + tan -1 y= tan -1 (x+ y)/(1-xy)

Now tan a = 1, tan b = 1/2 and tan c = 1/3

Now a + b +c = tan -1 ( 1) + tan-1 (1/2) + tan -1(1/3) =45 + tan-1 (( 1/2 +1/3)/(1-(1/2)x(1/3))) = 45 + tan-1(1)= 45+45= 90 degrees

tan (b+c) = (tan (b) + tan (c)) / (1-tan (b)*tan(c))

= (1/2 + 1/3) / (1 - (1/2)*(1/3))

= (5/6) / (1 - 1/6)

= (5/6)/(5/6)

= 1

Hence, (b+c) = 45 and (a+b+c) = 90

The first box is a square. Therefore, the triangle formed out of it is isosceles. hence each of the other opposite angle = 45 degrees. hence angle a = 45. Angle b = 30 Angle c = 15 a+b+C = 45+30+15 = 90

The solution is based on trigonometry

arctan(1)+arctan(1/2)+arctan(1/3) = 90d

$a$ is obviously $45°$ , $b=\arccos(\frac{2}{\sqrt{5}})=\arcsin(\frac{1}{\sqrt{5}}), c=\arccos(\frac{3}{\sqrt{10}})=\arcsin(\frac{1}{\sqrt{10}}).$ But $\cos(b+c)=\cos{b}\cdot{\cos{c}}-\sin{b}\cdot{\sin{c}}=\frac{\sqrt{2}}{2}$ so $a+b+c=90°$

When read your solutions I feel stupid haha. I don't know if it is right but I just divided 45 by 3 and it gives me 15, then: 45, 30, 15. And its sum is 90 haha.

I have seen this type of question first time andI solved this by only watching the question