3 squares
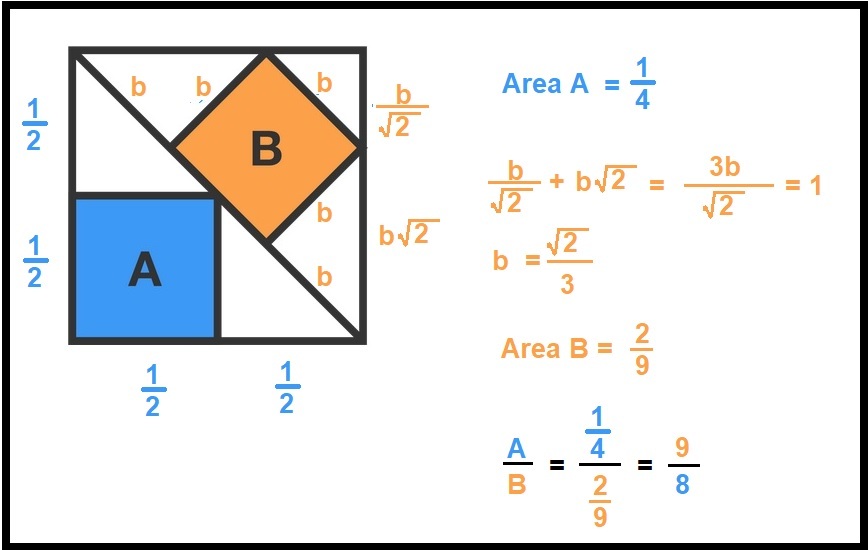
A diagonal divides a large, outer square into two equal parts. A smaller square is inscribed in each part. Let the area of the blue square be A , and let the area of the orange square be B .
What is B A ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Moderator note:
As pointed out in the comments, it's not entirely proven that the upper portion can be broken into 9 congruent triangles.
The premise gives enough information to say the marked triangle marked with a star above is a 45-45-90 one. This means it is isosceles and the two legs are congruent. This can then be used symmetrically on the other side of the square B to establish the length of the square of B is 1/3 of the diagonal of the entire square.
This implies a 3 by 3 grid can be laid down which intersects the points of B, leading to the 9 congruent triangle result.
To clarify, how do you know that the upper triangle can be cut into 9 triangles of equal areas as indicated?
Log in to reply
I suggest to you that it can be seen that the triangles must have the same dimensions and the same angles of 45 degrees, 45 degrees and 90 degrees, and so are congruent. What a fantastic solution this is! I got the same result but by calling the length of a side of square A as L and then finding the length of a side of square B. But this solution is extremely elegant!! Regards, David
The really briliant
How do you know which to cut in 4 and 9?
I don't follow why it is not entirely proven that the upper portion can be broken into 9 congruent triangles. The large square diagonal is at 45deg to the sides, therefore so are the sides of B (2 sides parallel and 2 perpendicular). If Lb is the length of each side of B, then the hypotenuses of the triangles adjacent to B are all Lb long, and all right-angle triangles with the other 2 angles of 45deg. The same can be said about the 4 triangles inside B. The remaining 2 triangles are also 90-45-45deg with the same length side. Therefore all 9 are congruent.
Total Down triangle is cut into two (½) not the small square
"A diagonal divides a large, outer square into two equal parts.." the diagonal does not necessarily have to be at 45 deg. However, if diagonal is limited in definition to 45 deg., then, as per the diagram above, the upper triangle can clearly (just visually) be divided into 9 congruent triangles. Given the discrete choice of answers, one must assume diagonal to mean 45 deg. Lay the 3x3 grid over the whole square and the upper triangle, along with the existing lines should make it pretty clear - see Thomas' post above.
Given the limited choices, I can tell what the answer is by looking at the sizes.
For the larger square we can say it has a side length of s.
For square A to fit and still be a square, it will need to have half the length of the original, or a side length of 2 1 s
so the area of square A is 4 1 s 2
For square B to fit and still be a square, we can split the diagonal of the big square into 3 equal pieces. To find the length of the diagonal we can use Pythagorean theorem or the 45-45-90 special right triangle rule, we can say that the diagonal has a length 2 s so the side length of square B is 3 2 s
This means the area of square B is 9 2 s 2
so the ratio of the areas B A is 9 2 s 2 4 1 s 2 which simplifies to 8 9
You can remove s by taking s=1
Log in to reply
That would only prove it for s=1. By having s cancel itself out you prove it for any value of s.
Log in to reply
Length is always relative. You can choose the unit of length to be the size of the square.
For your areas you should have s^2 "so the area of square A is 1/4 s^2" and the area of "B is 2/9 s^2. They still cancel in the ratio so the answer is the same, but s squared is required for the values as presented to be correct for the areas.
Log in to reply
Yes that would be correct, I carelessly overlooked that since it cancels in the end.
Without even using numbers, we see that Square A can be formed from the two triangles above and below it (this can be proven using the facts that a diagonal of a square bisects the 90 degree angles and that one of the legs of each triangle is also one of the sides of Square A) and leave no remaining parts, whereas Square B can be formed from the triangles beside it (this can be proven in the same way as explained for Square A) but leaves a remaining triangular part. So A is larger than B and the only valid answer is the third choice: 2A=.5 2B+c=.5 (where c is the remaining triangular part) 2A=2B+c»»»A=B+(c/2) A>B
How can you prove by your answer that remaining part of both halves isn't equal??
Square A's half does not leave any remaining part. For clarity: 2A=.5 2B+c=.5, where c is the remaining triangular part. Then, 2B+c=2A» B+(c/2)=A. A>B. I hope it's clear.
I don't think this is sufficient proof. The triangles around B are all smaller than the ones around A. So if B were sufficiently larger than A, it might compensate for the third tiny leftover-triangle you mentioned.
Log in to reply
No, bro. It can be easily seen from the equations I wrote some comments below that A is larger than B.
Here is a little visualization:
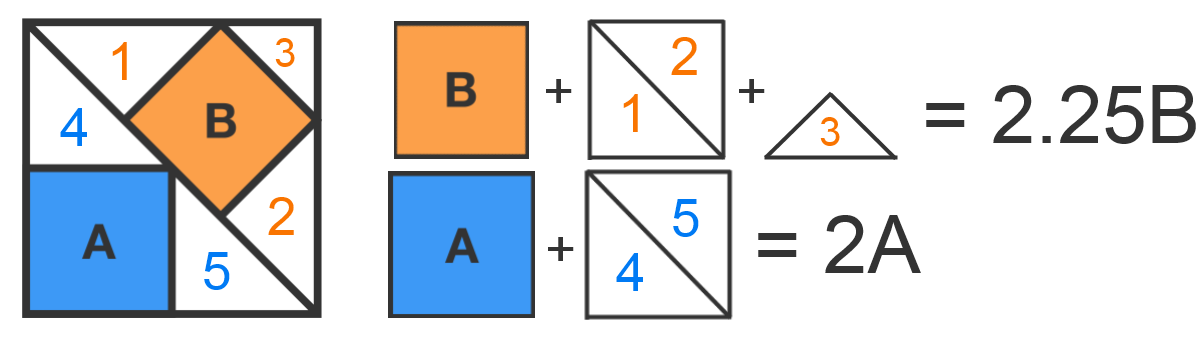 Because the upper and lower sum represent both a half of the triangle, it follows:
2
.
2
5
B
=
2
A
⇒
B
A
=
2
2
.
2
5
=
8
9
Because the upper and lower sum represent both a half of the triangle, it follows:
2
.
2
5
B
=
2
A
⇒
B
A
=
2
2
.
2
5
=
8
9
Firstly, we assume that the square pictured is a unit square. Then, notice that square
A
has side lengths of
2
1
. Given that information, we seek to find square
B
's side length, which we will label
x
. Additionally, we will label the length of the top left corner to the vertex of square
B
along the top edge
y
. The last piece of preliminary information we will use is that the length of half the diagonal, or from a corner to the vertex on square
A
along the diagonal, is
2
2
.
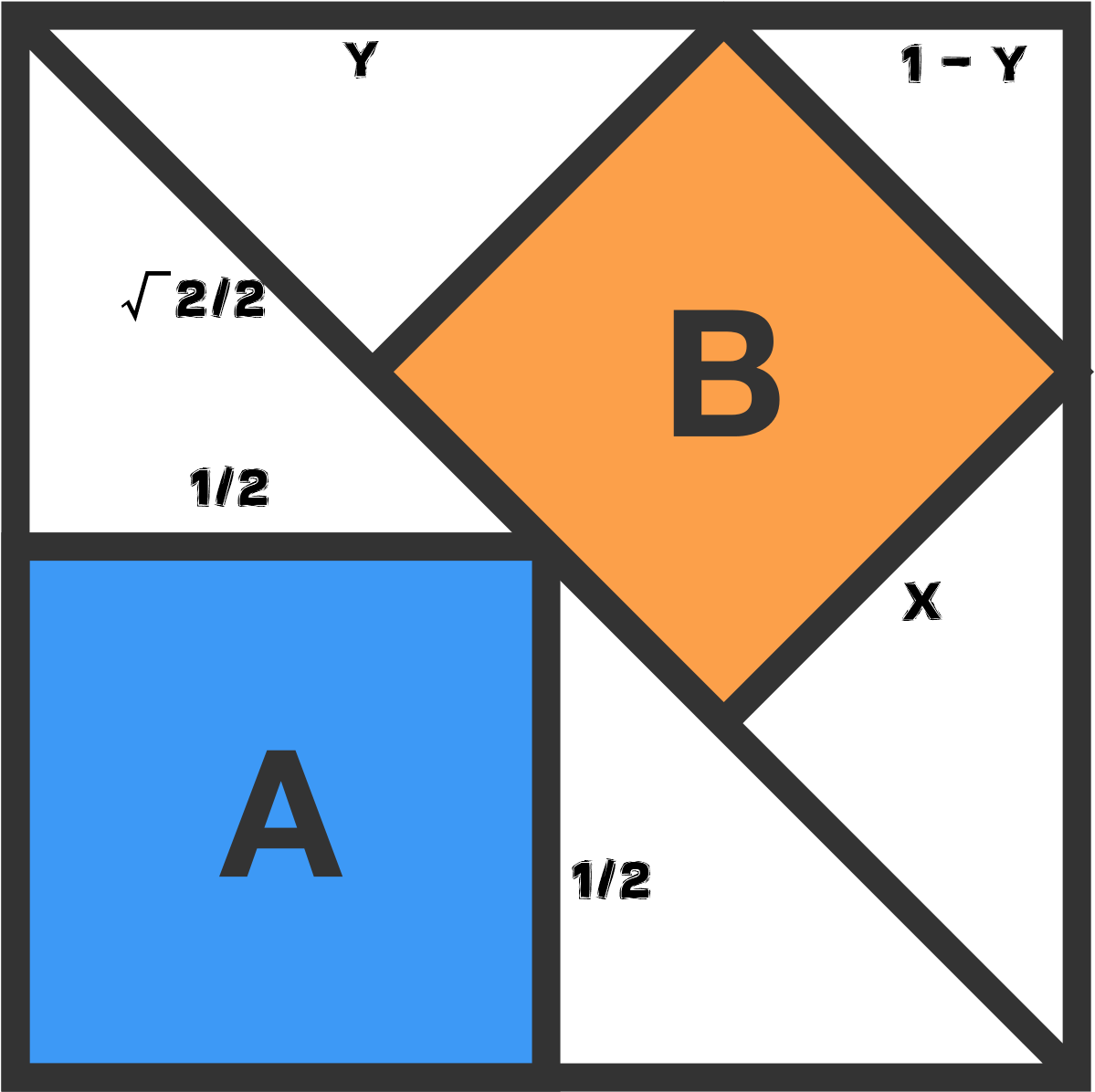 All triangles in this diagram are similar by angle-angle similarity because they are all
4
5
-
4
5
-
9
0
triangles. Therefore, by triangle similarity,
x
1
−
y
=
2
1
2
2
y
=
1
−
2
x
Then plugging the previous equation into another similarity proportion and we get
x
1
−
2
x
=
2
2
2
1
x
=
3
2
Thus, the area of square
A
is
4
1
and the area of square
B
is
9
2
. The ratio of
B
A
is then
9
2
4
1
=
8
9
.
All triangles in this diagram are similar by angle-angle similarity because they are all
4
5
-
4
5
-
9
0
triangles. Therefore, by triangle similarity,
x
1
−
y
=
2
1
2
2
y
=
1
−
2
x
Then plugging the previous equation into another similarity proportion and we get
x
1
−
2
x
=
2
2
2
1
x
=
3
2
Thus, the area of square
A
is
4
1
and the area of square
B
is
9
2
. The ratio of
B
A
is then
9
2
4
1
=
8
9
.
The statement said that A > B therefore A / B> 1 so that the only possible solution was 9/8. I know that it is not the most elegant solution, I have not done it either.
From the figure we can just observe that A is larger than B
I found the solution using triangle congruencies and defining the sides of A as X. By using the triangle congruencies, I found that the big triangle that square A is in has side length of 2X, and therefore all the sides of the big square are 2x. I will attach a picture of my work (Sorry its a bit messy):
Let the sides of box A be of length a, and the sides of box B be of length b. Observe that A's side divides evenly the side of the square, so that the square's side is of length 2a. So then the diagonal of the square has a squared length of 8A. That same diagonal has a length of 3b, or it's square 9B. So 8A = 9B, and A/B = 9/8
let L=the length of the largest square,
A=( 2 L )^2= 4 L 2
We can cut the top left side of the diagonal into 9 identical triangles to show that sqrt(B) is 3 d i a g o n a l
B=( 3 d i a g o n a l )^2=( 3 s q r t ( 2 L 2 ) )^2= 9 2 L 2
A* B 1 = 4 ∗ 2 L 2 L 2 ∗ 9 = 8 9
:-)
The length of one side of the square in the lower half(A) is half of the size of the length of the outer square. Therefore area of square A is 4 a 2 . Length of one side of the square in the upper half (B) is one third of the diagonal of the outer square. Therefore area of square B is 9 2 a 2 . Therefore B A equals 8 9 .
The whole square (let's call it S ) is split into two equal halves. Taking the half with the square A , we notice that it is comprised of A as well as two other sections, t 1 and t 2 . A is a square extending from the corner of S to its diagonal, and therefore it is a quarter of S , and thus half of the right triangle made by the diagonal. Triangles t 1 and t 2 , then, also together form half the right triangle. So we can say t 1 + t 2 = 4 1 S = A . Together, the left triangle half can be written as A + t 1 + t 2 = A + A , or 2 A .
As for the right half, it is comprised of square B and three triangles: t 3 and t 4 , which are identical, and t 5 in the corner. Noticing that t 5 can be folded down onto the intersection of the diagonals of B informs us that t 5 = 4 1 B , because it can only cover a fourth of the area. Likewise, triangles t 3 and t 4 can be folded across B , and each take up half of the area of B . So t 3 = t 4 = 2 1 B . The right half of square S , then, is written B + t 3 + t 4 + t 5 = B + 2 1 B + 2 1 B + 4 1 B , which simplifies to 4 9 B .
Finally, since each half of S is equivalent, we can set the left half, 2 A , equal to the right half, 4 9 B . So, 2 A = 4 9 B , and rearranging gives us B A = 8 9 .
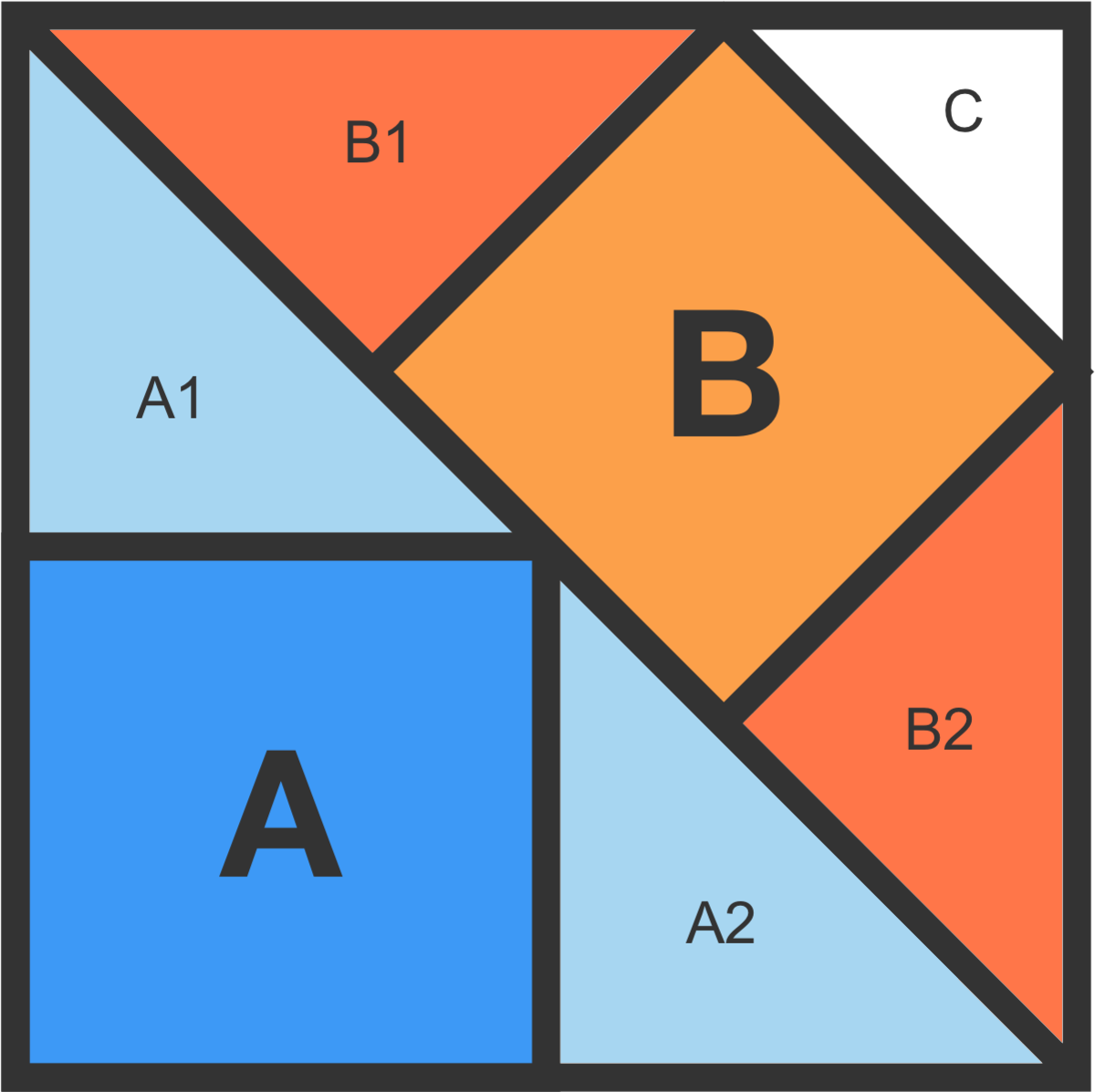
A can be formed using A1 and A2, and B can be formed using B1 and B2. Since the two halfs of the square are equal, we have
A + A 1 + A 2 2 A A A / B = B + B 1 + B 2 + C = 2 B + C = B + 2 C > B > 1
(where the labels represent the areas of the geometric object)
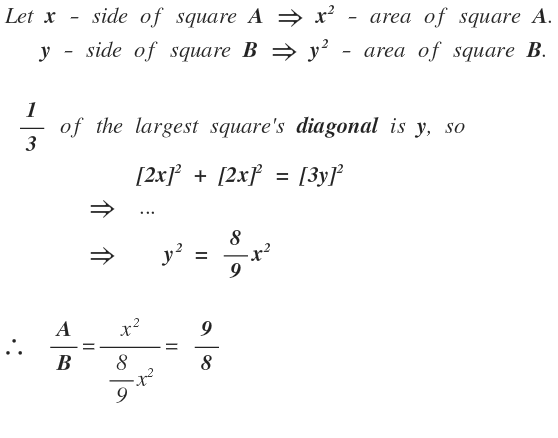
Cut the lower half and the upper one into respectively 4 and 9 triangles of equal areas, as below.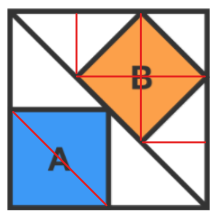
Then A = 2 1 and B = 9 4 , so B A = 2 1 4 9 = 8 9