3-Way Chamfer

Geometry Level 3

A wooden cube with a side length of 10 cm is subject to 3 consecutive chamfers along three edges that meet in a single vertex. Each chamfer is angled at 4 5 ∘ 45^{\circ} with the faces of cube that join at the chamfer edge. The chamfer indents a distance of 2.5 cm along each of these two faces.

Find the volume of wood (in cm 3 \text{cm}^3 ) that was cut out by the three chamfers. If the volume is V V then enter ⌊ 1 0 5 V ⌋ \lfloor 10^5 V \rfloor .


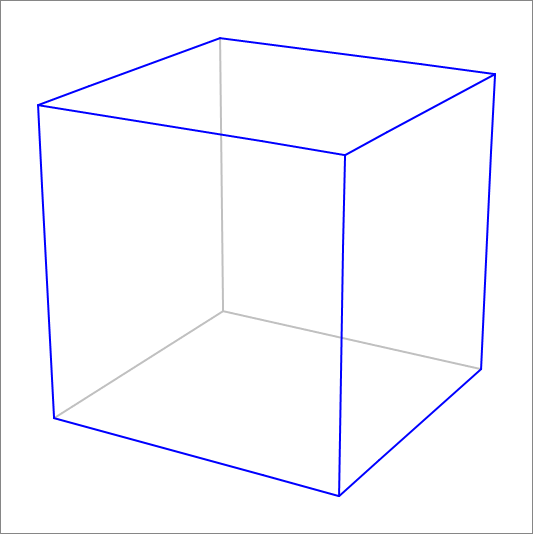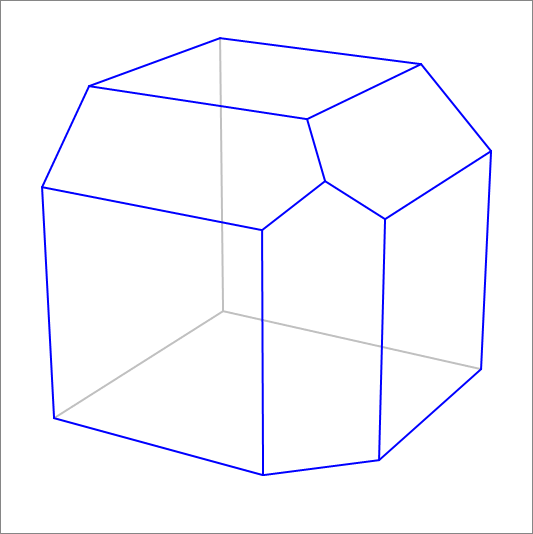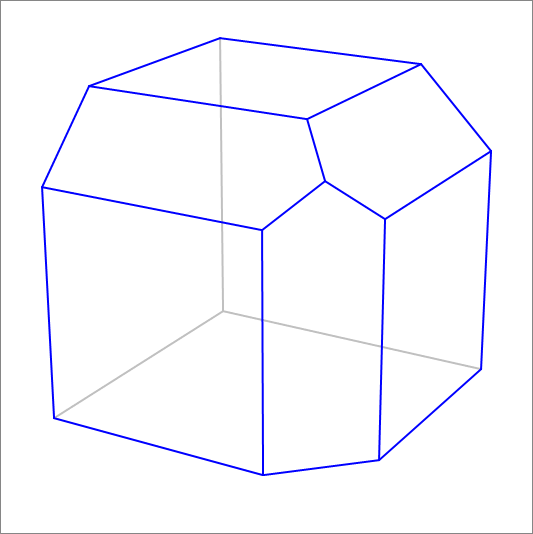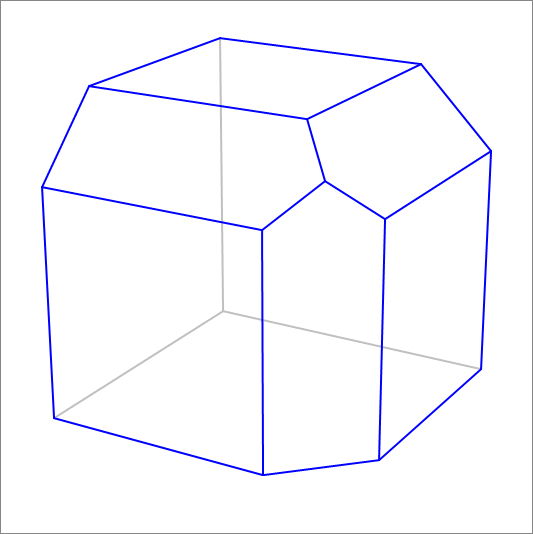
The answer is 8203125.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Brute force: Volume [ RegionUnion [ RegionIntersection [ Cuboid [ { − 5 , − 5 , − 5 } , { 5 , 5 , 5 } ] , HalfSpace [ { 0 , − 1 , − 1 } , { 0 , 15 4 , 15 4 } ] ] , RegionIntersection [ Cuboid [ { − 5 , − 5 , − 5 } , { 5 , 5 , 5 } ] , HalfSpace [ { − 1 , 0 , − 1 } , { 15 4 , 0 , 15 4 } ] ] , RegionIntersection [ Cuboid [ { − 5 , − 5 , − 5 } , { 5 , 5 , 5 } ] , HalfSpace [ { − 1 , − 1 , 0 } , { 15 4 , 15 4 , 0 } ] ] ] ] ⇒ 2625 32 \text{Volume}\left[\text{RegionUnion}\left[ \\ \text{RegionIntersection}\left[\text{Cuboid}[\{-5,-5,-5\},\{5,5,5\}],\text{HalfSpace}\left[\{0,-1,-1\},\left\{0,\frac{15}{4},\frac{15}{4}\right\}\right]\right], \\ \text{RegionIntersection}\left[\text{Cuboid}[\{-5,-5,-5\},\{5,5,5\}],\text{HalfSpace}\left[\{-1,0,-1\},\left\{\frac{15}{4},0,\frac{15}{4}\right\}\right]\right], \\ \text{RegionIntersection}\left[\text{Cuboid}[\{-5,-5,-5\},\{5,5,5\}],\text{HalfSpace}\left[\{-1,-1,0\},\left\{\frac{15}{4},\frac{15}{4},0\right\}\right]\right]\right]\right] \Rightarrow \frac{2625}{32}

Volume of a single chamfer is 125 4 \frac{125}{4} .

Volume of intersection of 2 chamfers is 125 24 \frac{125}{24} .

Volume of intersection of all 3 chamfers is 125 32 \frac{125}{32} .

3 × 125 4 − 3 × 125 24 + 125 32 ⇒ 2625 32 ⇒ 82 1 32 3\times\frac{125}{4}- 3\times\frac{125}{24} + \frac{125}{32} \Rightarrow \frac{2625}{32} \Rightarrow 82\frac{1}{32} as an improper fraction.

The first expression is in Wolfram Mathematica 12 language, which is not the same as Wolfram/Alpha.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...