#30 of June 2015 Grade 10 CSAT(Korean SAT) mock test

Geometry Level 5

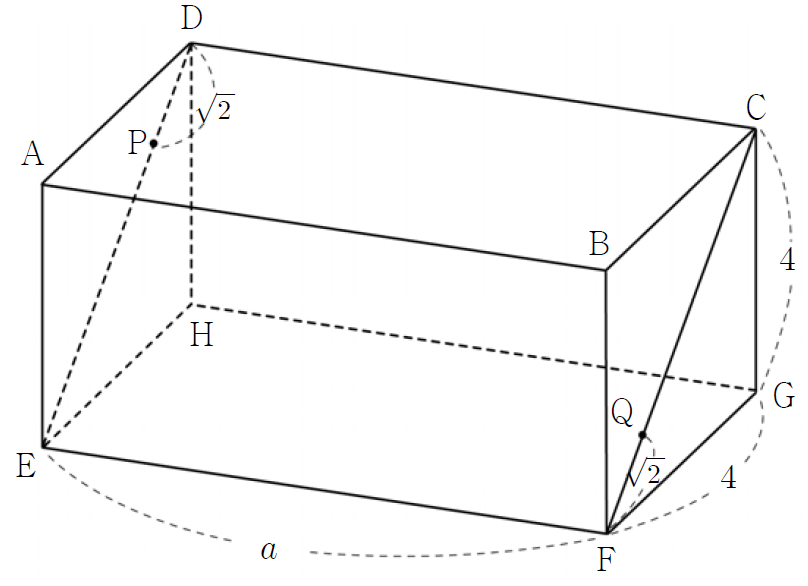
As shown above, there is a rectangular parallelepiped $\text{ABCD-EFGH}$ whose height is $4$ and base plane's two sides are $a(a>5)$ and $4$ .

Point $\text{P}$ and $\text{Q}$ are on $\overline{\text{DE}}$ and $\overline{\text{CF}}$ respectively, satisfying $\overline{\text{DP}}=\overline{\text{FQ}}=\sqrt{2}$ .

Starting from point $\text{P}$ , the shortest distance of traveling towards point $\text{Q}$ , with only moving along the surface of the parallelepiped, is $2\sqrt{34}$ .

Find the value of $30a$ .

This problem is a part of <Grade 10 CSAT Mock test> series .

The answer is 240.

1 solution

Boi (보이)
Jun 8, 2017

There are $2$ paths that travel from point $P$ to point $Q$ that should be considered.

$\text{i)}$ moving like below

Planar figure of the picture is shown below.

$\overline{PQ}=\sqrt{a^2+8a+20}$

$\text{ii)}$ moving like below

Planar figure of the picture is shown below.

$\overline{PQ}=\sqrt{a^2+4a+40}$

Since $(a^2+4a+40)-(a^2+8a+20)=-4a+20<0$ , case $\text{ii)}$ is the correct path.

$\sqrt{a^2+4a+40}=2\sqrt{34} \\ a^2+4a+40=136 \\ (a-8)(a+12)=0 \\ a=8 \text{ }(\because a>0)$

Therefore

$30a=\boxed{240}$

Nice solution. I hadn't thought of the second path, so I learned something new. :)

Brian Charlesworth - 3 years, 12 months ago

Glad you could learn something! :D

Boi (보이) - 3 years, 12 months ago

This should be rather a grade 8 problem.

D K - 2 years, 9 months ago