300 followers problem! Conics!

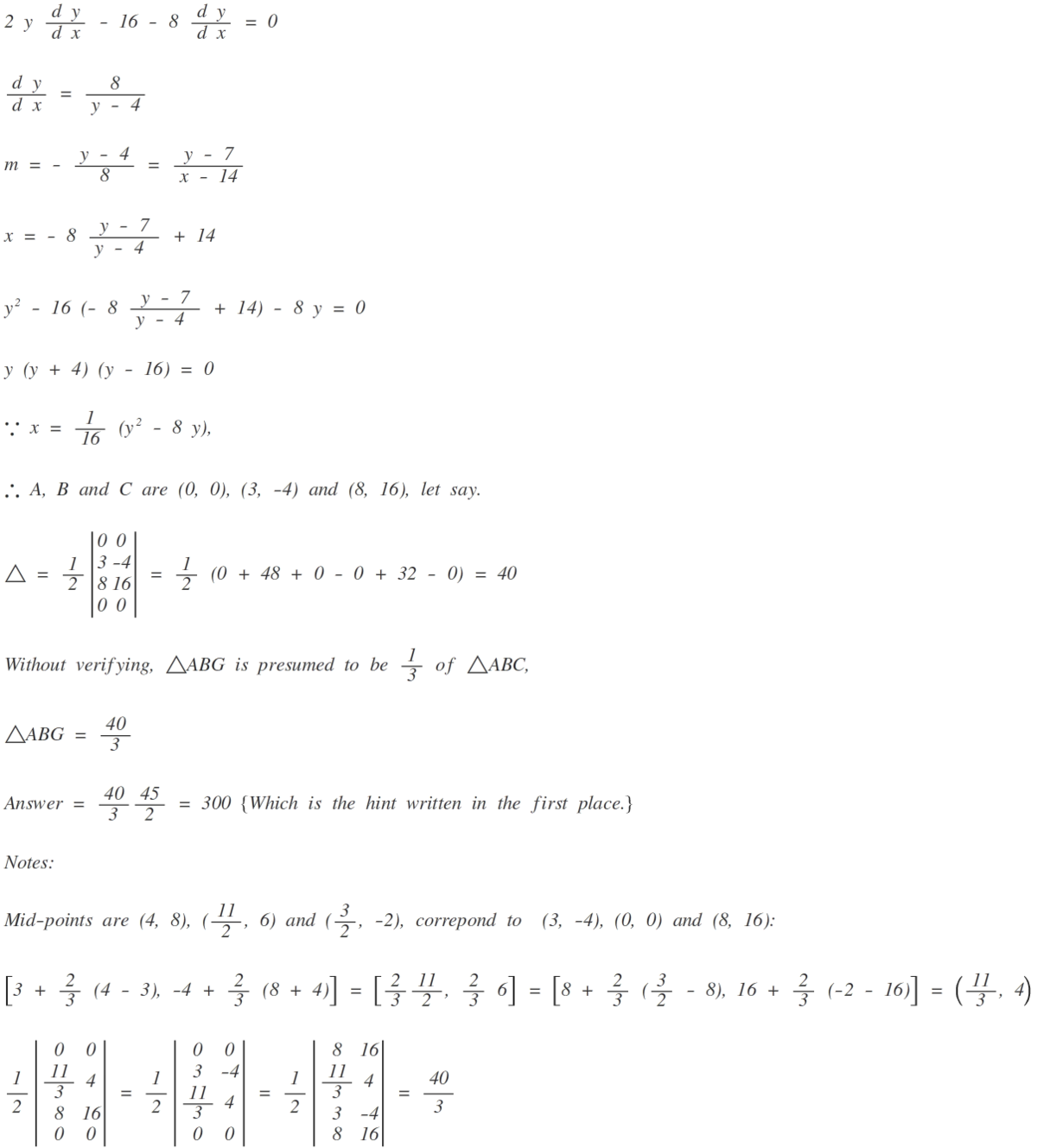
Lets try to convert equation of parabola to standard form.

$y^2-16x-8y=0\\(y-4)^2=16(x+1)=0$

Defining new coordinates as $Y=y-4, X=x+1$ , we get,

$Y^2=16X$

Now assume a general point on this parabola be $(4t^2,8t)$ where 't' is the parameter.

Point $P$ in new coordinate system becomes $P(15,3)$ .

A general equation of normal from a point $(4t^2,8t)$ is $y+tx=8t+4t^3$ .

Substituting $P$ in this equation,

$3+15t=8t+4t^3\\4t^3-7t-3=0\\(t+1)(2t+1)(2t-3)=0\\t=-1,\frac{-1}{2},\frac{3}{2}$

So the points will be $A(9,12),B(4,-8),C(1,-4)$

Using determinants, we can calculate area of $\triangle ABC$ as $40$

Now, since $G$ is centroid, $\alpha =\triangle ABG=\dfrac{\triangle ABC}{3}=\dfrac{40}{3}$

$\dfrac{45}{2}\alpha =\dfrac{45}{2}×\dfrac{40}{3}=300$

One simple yet interesting thing to note is the fact that area of a closed curve is independent of origin. Thus, transformation made no change to our answer.