300 Followers question!

We can do this by eradicating cases.

If $\alpha>0$ we see that whole expression always remains positive.

If $\alpha<-1$ we see that $300x^{299}$ becomes too much large for the expression to be zero , making the polynomial always negative.

So we can easily conclude that $-1<\alpha<0$ and hence $\lfloor \alpha \rfloor = -1$

Let $f(x) = 300x^{299}+299x^4+343x^3+23x+300$ . We note that: $f(0) = 300$ and $f(-1) = -67$ . Therefore, there is a real root of $f(x)$ in $-1<x<0$ . And this is the only root because for $x<-2$ or $x>2$ , $f(x) \approx 300x^{299}$ a constantly increasing function. Therefore, $-1< \alpha < 0\quad \Rightarrow \lfloor \alpha \rfloor = \boxed{-1}$ .

The following graph shows the real root $\alpha$ .

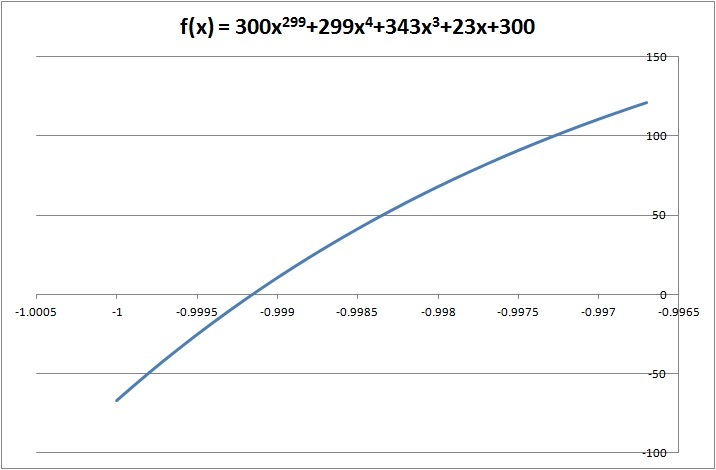
By observation, it is clear that the root is negative as the expression is positive for x>0 and equals 300 at x=0.Now by some hit and trial f(-1)<0 => f(0)*f(-1)<0=> The real root lies between -1 and 0 => [alpha]=-1