300 Followers Problem

Calculus Level 3

The Value of the integral

∫ − 1 3 \displaystyle\int_{-1}^{3} ( ∣ x ∣ + ∣ x − 1 ∣ ) (|x|+|x-1|) d x dx


The answer is 9.

Parth Lohomi by Parth Lohomi , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

I don't think this is a level 5 problem, just done it by area under curve

2 Helpful 0 Interesting 0 Brilliant 0 Confused

You're right-this is an easy (very easy) calculus problem. It should be Level 2.

bobby jim - 6 years, 5 months ago
Prakhar Gupta
Jan 12, 2015

This can also be done by breaking the limits of integrals so that we can remove the modulus sign. The given integral is:- ∫ − 1 3 ( ∣ x ∣ + ∣ x − 1 ∣ ) d x \int_{-1}^{3} (|x|+|x-1|) dx This can be broken into 3 3 parts as follows:- = ∫ − 1 0 ( − x + 1 − x ) d x + ∫ 0 1 ( x + 1 − x ) d x + ∫ 1 3 ( x + x − 1 ) d x =\int_{-1}^{0}(-x+1-x) dx + \int_{0}^{1}(x+1-x) dx + \int_{1}^{3} (x+x-1) dx Now we have removed the modulus sign and we can integrate it easily and get the answer 9 9 .

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Masbahul Islam
Dec 31, 2014

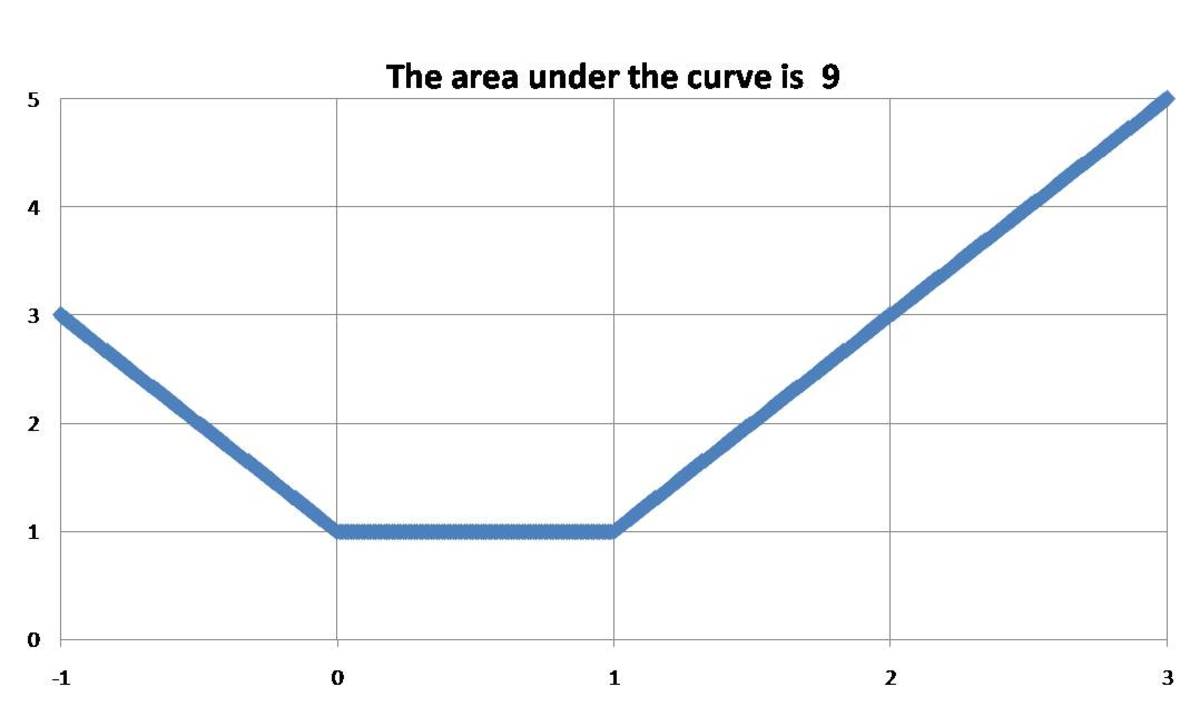The area under the curve is 9

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...