Heat exchanged in a cyclic process

Classical Mechanics Level 3

One mole of ideal monoatomic gas is taken round the cyclic process A B C A ABCA . The following is a schematic P V PV graph of a process A B C A ABCA .

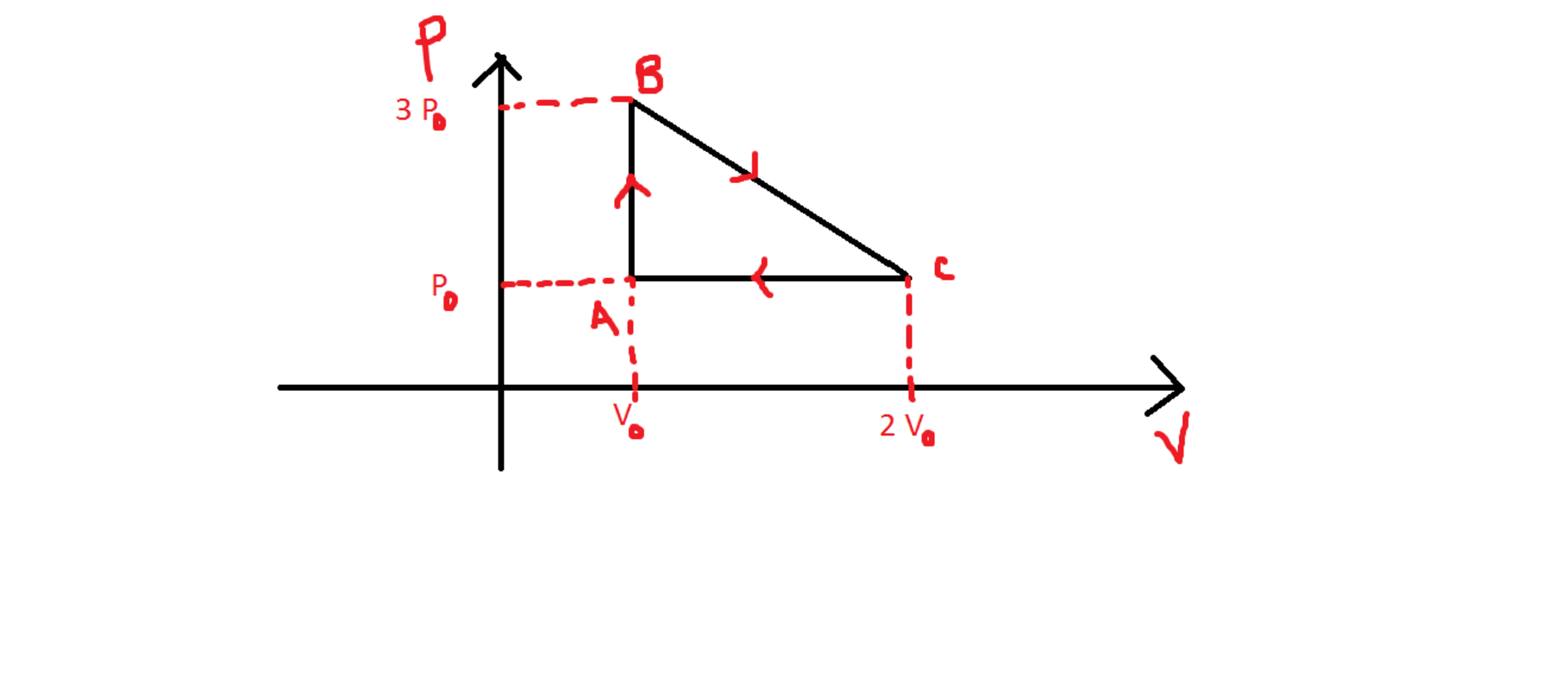
Find the heat exchange in the process A B AB .

9 P 0 V 0 2 \dfrac{9P_0V_0}{2} 3 P 0 V 0 3P_0V_0 − 3 P 0 V 0 -3P_0V_0 3 P 0 V 0 2 \dfrac{3P_0V_0}{2}

Md Zuhair by Md Zuhair , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ayon Ghosh
Apr 22, 2017

In an isochoric process,

d Q dQ = d U dU + + d W dW

( here d is short for delta not differential)

But d U dU = u C v d T u C_v dT = C v d T C_v dT

(u is short for mu - no. of moles =1 )

Also d W dW = P d V PdV = 0 0 since d V dV = 0 0 for an isochoric process.

Hence d Q dQ = d U dU = C v d T C_v dT

From Ideal gas equation, we get,

d T dT = d P V dPV / / R R ( since u =1 )

Substituting,

d Q dQ = C v d P V C_v dPV / / R R = 3 / 2 R ∗ 2 P ∗ V 3/2 R * 2P * V / / R R = 3 P V 3PV

( because for monoatomic ideal gases gamma = C p C_p / / C v C_v = 5 / 3 5/3 and also C p C_p - C v C_v = R R from which we get C p C_p = 3 / 2 3/2 )

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...