3D B and E Fields (part 2)
A particle of mass m and charge q is positioned at the origin at time t = 0 .Its initial velocity and initial acceleration are v and a respectively. There are electric and magnetic fields E and B throughout space.
How far from the origin is the particle at time t = 1 5 ?
Bonus: Plot the trajectories in the x y , y z and z x planes
Details and Assumptions
1)
m
=
1
2)
q
=
+
2
3)
E
=
(
E
x
,
E
y
,
E
z
)
=
(
3
,
4
,
5
)
4)
B
=
(
B
x
,
B
y
,
B
z
)
=
(
6
,
7
,
8
)
5)
v
=
(
v
x
,
v
y
,
v
z
)
=
(
9
,
1
0
,
1
1
)
6)
a
=
(
a
x
,
a
y
,
a
z
)
=
(
1
2
,
1
3
,
1
4
)
The answer is 1845.732.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath
sir this problem is clearly stated or not??

Thanks in advance.
Log in to reply
Apart from one typo in the problem, a is not clearly defined. I would guess that a is the distance between the circle centre and the point charge along its axis.
@Karan Chatrath
hello sir, I am Neeraj only. Due to some reasons I have changed my name.
Recently, I have posted a new problem Complex flux,
Two members have posted the solution, the 2nd one is Novak sir,
But I am not able to understand his solution and that solution seems me interesting and I am curious about it.
Can you help me to understand that solution's first 2 paragraphs.
Thanks in advance.
Log in to reply
I have not yet attempted that problem. When I do, I will take a look at the solutions.
@Karan Chatrath
I have now seen your report sincerely.
I would talk to you before what is your mistake, but I am such a lazy person, even I didn't look at your solution.
I just go to Mr chase.
So, the mistake in your solution is The particle doesn't have to go to that corner of capacitor.
It have to lift up. My English is not good so let me explain in hindi.
Jaise electron niche jaayega to gravity lagega, par thode time baad usme inta electric force lag jaayega ki vo fir se upar chadh jaayega.
Like this
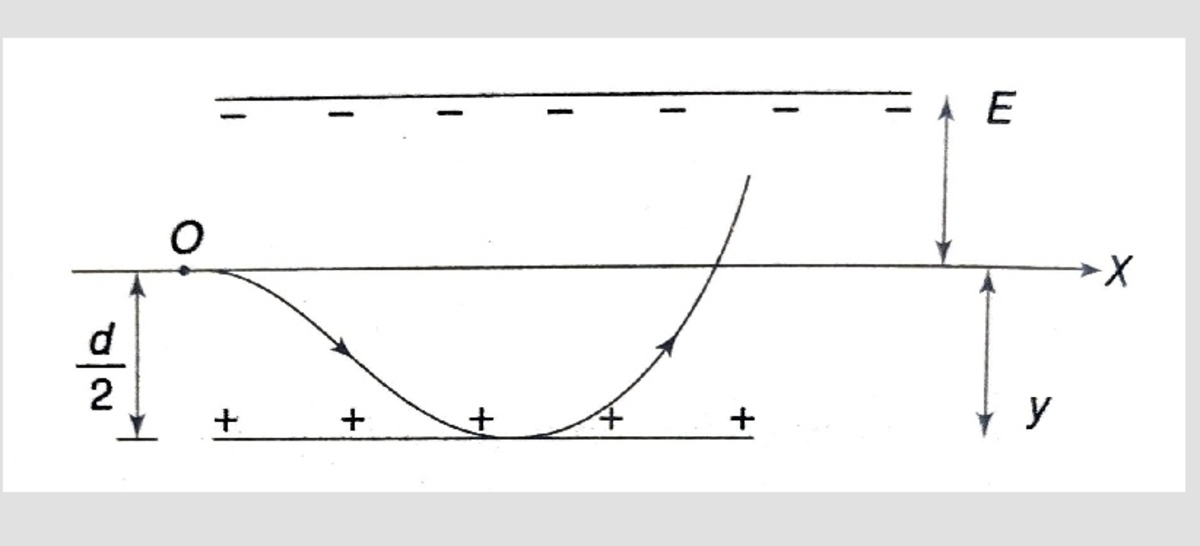
Log in to reply
Okay, I understand your point. I will attempt it again later. Thanks for the clarification
Code-based solution. Done using MATLAB: