3D E and B Fields (Corrected)
A particle of mass m and charge q is positioned at the origin at time t = 0 . Its initial velocity is v 0 . There are electric and magnetic fields E and B throughout space.
How far from the origin is the particle at time t = 5 ?
Bonus: Plot the trajectories in the x y , y z , and z x planes
Details and Assumptions:
1)
m
=
2
2)
q
=
+
1
3)
v
0
=
(
v
0
x
,
v
0
y
,
v
0
z
)
=
(
−
1
,
1
,
2
)
4)
E
=
(
E
x
,
E
y
,
E
z
)
=
(
1
,
−
2
,
3
)
5)
B
=
(
B
x
,
B
y
,
B
z
)
=
(
4
,
8
,
−
2
)
The answer is 12.42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Applying Newton's second law gives:
m a = q E + q ( v × B )
2 ⎣ ⎡ x ¨ y ¨ z ¨ ⎦ ⎤ = ⎣ ⎡ 1 − 2 3 ⎦ ⎤ + ⎝ ⎛ ⎣ ⎡ x ˙ y ˙ z ˙ ⎦ ⎤ × ⎣ ⎡ 4 8 − 2 ⎦ ⎤ ⎠ ⎞
Simplifying gives:
x ¨ = 2 1 − 4 z ˙ − y ˙ y ¨ = − 1 + x ˙ + 2 z ˙ z ¨ = 2 3 + 4 x ˙ − 2 y ˙
Now, knowing the equations of motion and the initial conditions, the Laplace transform can be taken on both sides, which converts the above differential equations to linear equations in the s-domain. To perform the Laplace transform, one may search the internet for a 'table of standard Laplace transforms'. The equations are:
s 2 X + s Y + 4 s Z = 2 s 1 − 1 − s X + s 2 Y − 2 s Z = − s 1 + 1 − 4 s X + 2 s Y + s 2 Z = 2 s 3 + 2
Here, X , Y and Z are the laplace transforms of the functions x ( t ) , y ( t ) and z ( t ) . Solving for X , Y and Z gives:
X = − 2 s 3 ( s 2 + 2 1 ) 2 s 3 + 1 7 s 2 + 1 0 s + 1 8 Y = 2 s 3 ( s 2 + 2 1 ) 2 s 3 + 4 s 2 + 7 s − 3 6 Z = 2 s 3 ( s 2 + 2 1 ) 4 s 3 − 9 s 2 + 8 s + 9
Now, all that needs to be done is the computation of the inverse Laplace transform of the above expressions. This can be done by using:
https://www.wolframalpha.com/widgets/view.jsp?id=7c762190486dfb47dca59a9a1f8cb1a8
The resulting solutions of the differential equations are:
x ( t ) = 2 9 4 1 1 3 cos ( 2 1 t ) − 2 1 5 t − 4 4 1 1 6 2 1 sin ( 2 1 t ) − 1 4 3 t 2 − 2 9 4 1 1 3 y ( t ) = 6 t − 1 4 7 2 0 cos ( 2 1 t ) + 1 2 6 5 2 1 sin ( 2 1 t ) − 7 3 t 2 + 1 4 7 2 0 z ( t ) = 2 1 4 t + 4 9 1 1 cos ( 2 1 t ) + 4 4 1 3 8 2 1 sin ( 2 1 t ) + 2 8 3 t 2 − 4 9 1 1
Substituting t = 5 and simplifying and computing the distance between the origin and the point of interest, gives the required answer. The trajectory of the particle can be studied as such:
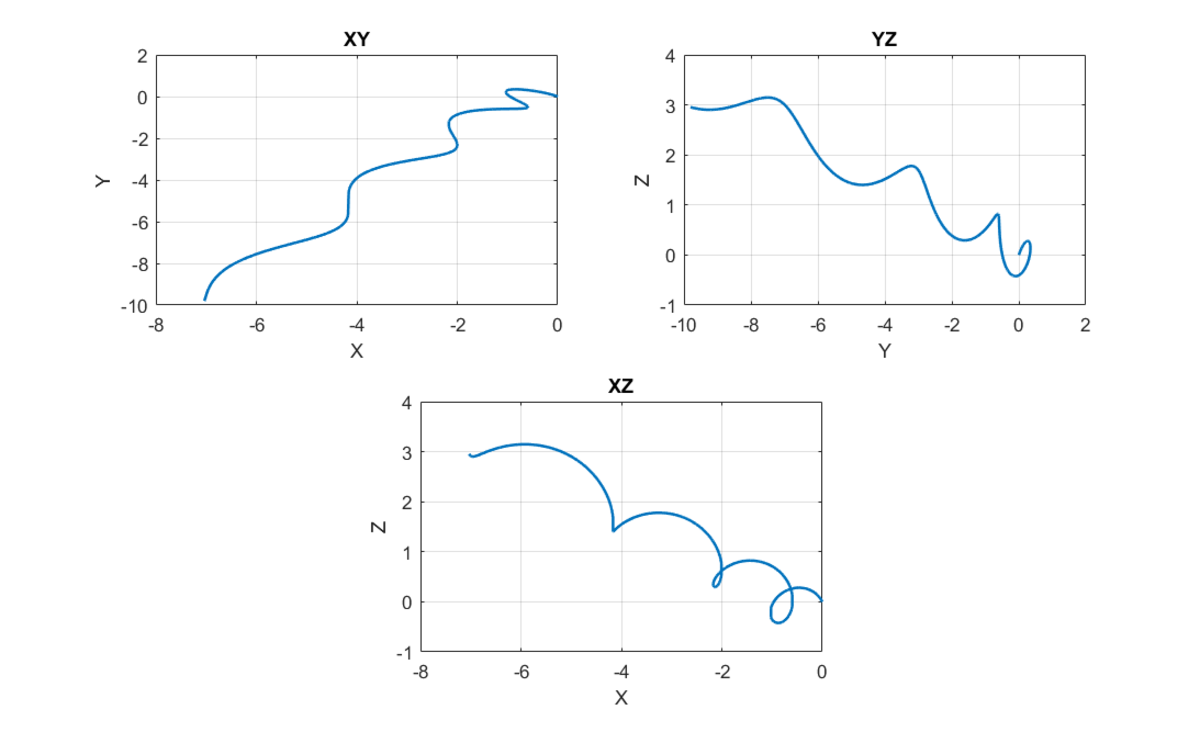
Amazing, with the Laplace Transform you indeed get a much more accurate result than by numerically solving. It's such a powerful tool, and implementing Euler integration for the above system would be inaccurate even for very small time-steps.
@Karan Chatrath
Now I am able to understand your solution very well.
And your solution was previously upvoted.
Thankyou so much.
I'm very impressed by the solution provided by @Karan Chatrath, in which a linear system is solved to get the Laplace equation for each dimension, and then the inverse transformations are applied. For the sake of completeness, I will upload the numerical solution as well. This results in the same trajectories and final answer as the Laplace method.