3D Marion's Theorem

Geometry Level 3

This problem can be viewed as the 3D analog of Marion's theorem .

Imagine that each edge of a tetrahedron is trisected. Then, through each of these 12 points and its two opposite vertices, a plane is constructed for a total of 12 planes.

Now, let $V$ denote the volume of the tetrahedron, and $V_M$ the volume of the 3D figure carved out by the 12 planes inside the tetrahedron. If $V_M=\frac{A}{B}V,$ where $A$ and $B$ are coprime positive integers, find $A+B.$

The 3D figure in question is shown below:

The answer is 36.

5 solutions

Mark Hennings
Feb 27, 2018

Start with a tetrahedron whose base lies in the $xy$ -plane, with one vertex at the origin. Applying two shears, one parallel to the $xz$ -plane and one parallel to the $yz$ -plane, and possibly a rotation about the $z$ -axis, we can convert the tetrahedron to one whose base has vertices $(0,0,0)$ , $(a,0,0)$ , $(0,b,0)$ for some $a,b > 0$ . Applying further shears parallel to the $xy$ -plane will keep the base fixed and shift the top vertex to $(0,0,c)$ for some $c>0$ (again, a rotation might be needed to make $c$ positive).

Shears and rotations preserve volumes, map planes to planes, and points of trisection on a line are mapped to points of trisection on the image line. Thus the ratio of $V_M$ to $V$ is the same for the original tetrahedron and the new tetrahedron.

Since scalings transform volumes in a predictable manner, and also map planes to planes and preserve trisections, we deduce that the ratio of $V_M$ to $V$ is the same for all tetrahedra, being equal to the ratio of $V_M$ to $V$ for the tetrahedron with vertices $(0,0,0)$ , $(3,0,0)$ , $(0,3,0)$ , $(0,0,3)$ .

For this case, $V = \tfrac92$ , and Mathematica tells me that $V_M = \tfrac{9}{70}$ . Thus the ratio of $V_M$ to $V$ is $\tfrac{1}{35}$ , making the answer $1+35=\boxed{36}$ .

Did u qualify olympiads!!! Man I am Amazed; It is hrd for me to get my heads close to the 2d version & u solved te 3d problem!!!!

Ariijit Dey - 3 years, 3 months ago

Please don't talk like a mentally disabled person. If you're here then you probably aren't one.

Vilim Lendvaj - 3 years, 3 months ago

Your first three paragraphs are trivial. I tried with the same vertices.
How did you find Vm? Not having used Mathematica, I almost consider it cheating, but how did you implement? What's the best way to do this by hand?

Jeremy Galvagni - 3 years, 3 months ago

Not so much trivial as elementary. These paragraphs show that it is sufficient to answer the problem for a specific tetrahedron, one which is readily susceptible to calculation.

The 2d Marion Theorem is proved using barycentric coordinates. There is a 3D version of barycentric coordinates based around a tetrahedron, and I suspect that this theorem could be proved using them.

Mark Hennings - 3 years, 3 months ago

I agree with Jeremy.

YAG G - 3 years, 2 months ago

Sharon Devlin
Mar 7, 2018

I took the 12 sides and multiplied them by 3 as in 3D 12 ×3=36

证明过程太少了，能不能多写一点证明一下

许宏量 - 3 years, 2 months ago

David Vreken
Mar 8, 2018

The points $(0, 3\sqrt{2}k, 3k)$ , $(3\sqrt{2}k, 0, -3k)$ , $(0, -3\sqrt{2}k, 3k)$ , and $(-3\sqrt{2}k, 0, -3k)$ are coordinates of a regular tetrahedron with side lengths of $6\sqrt{2}k$ and a volume of $V = 72k^3$ that is centered about the origin.

The points of trisection on each side are:

$(\sqrt{2}k, 2\sqrt{2}k, k)$	$(2\sqrt{2}k, \sqrt{2}, -k)$	$(-\sqrt{2}k, 2\sqrt{2}k, k)$	$(-2\sqrt{2}k, \sqrt{2}k, -k)$
$(0, \sqrt{2}k, 3k)$	$(0, -\sqrt{2}k, 3k)$	$(-2\sqrt{2}k, -\sqrt{2}k, -k)$	$(-\sqrt{2}k, -2\sqrt{2}k, k)$
$(\sqrt{2}k, -2\sqrt{2}k, k)$	$(2\sqrt{2}k, -\sqrt{2}k, -k)$	$(\sqrt{2}k, 0, -3k)$	$(-\sqrt{2}k, 0, -3k)$

That means the $12$ trisecting planes have the equations:

$\sqrt{2}x - 2\sqrt{2}y + 3z = -3k$	$2\sqrt{2}x - \sqrt{2}y + 3z = 3k$	$2\sqrt{2}x + \sqrt{2}y - 3z = -3k$
$\sqrt{2}x + 2\sqrt{2}y - 3z = 3k$	$3\sqrt{2}x + z = 3k$	$3\sqrt{2}x - z = -3k$
$2\sqrt{2}x - \sqrt{2}y - 3z = -3k$	$\sqrt{2}x - 2\sqrt{2}y - 3z = 3k$	$2\sqrt{2}x + \sqrt{2}y + 3z = 3k$
$\sqrt{2}x + 2\sqrt{2}y + 3z = -3k$	$3\sqrt{2}y - z = 3k$	$3\sqrt{2}y + z = -3k$

Each vertex of the center figure can be found by carefully solving the intersection of three of the above planar equations, and are:

$(-\frac{\sqrt{2}}{2}k, \frac{\sqrt{2}}{2}k, 0)$	$(0, 0, k)$	$(\frac{\sqrt{2}}{2}k, \frac{\sqrt{2}}{2}k, 0)$
$(-\frac{\sqrt{2}}{2}k, -\frac{\sqrt{2}}{2}k, 0)$	$(0, 0, -k)$	$(\frac{\sqrt{2}}{2}k, -\frac{\sqrt{2}}{2}k, 0)$
$(-\frac{3\sqrt{2}}{7}k, 0, \frac{3}{7}k)$	$(0, \frac{3\sqrt{2}}{7}k, -\frac{3}{7}k)$	$(\frac{3\sqrt{2}}{7}k, 0, \frac{3}{7}k)$
$(-\frac{3\sqrt{2}}{5}k, 0, -\frac{3}{5}k)$	$(0, -\frac{3\sqrt{2}}{5}k, \frac{3}{5}k)$	$(\frac{3\sqrt{2}}{5}k, 0, -\frac{3}{5}k)$
$(0, \frac{3\sqrt{5}}{5}k, \frac{3}{5}k)$	$(0, -\frac{3\sqrt{2}}{7}k, -\frac{3}{7}k)$

These points form a dodecahedron with congruent kite faces, with shorter sides of $\frac{\sqrt{34}}{7}k$ , longer sides of $\frac{\sqrt{22}}{5}k$ , and diagonals of $\sqrt{2}k$ and $\frac{6\sqrt{38}}{35}k$ . The vertices that are the intersection of the two shorter sides are $\frac{3\sqrt{3}}{7}k$ units away from the origin, the vertices that are the intersection of the two longer sides are $\frac{3\sqrt{3}}{5}k$ units away from the origin, and all other vertices are $k$ away from the origin.

This dodecahedron can be split into $24$ congruent tetrahedrons, where each base is the triangle formed by the symmetric half of the kite face and each vertex is at the origin, so each tetrahedron has six side lengths of $\frac{6\sqrt{38}}{35}k$ , $\frac{\sqrt{34}}{7}k$ , $\frac{\sqrt{22}}{5}k$ , $\frac{3\sqrt{3}}{7}k$ , $\frac{3\sqrt{3}}{5}k$ , and $k$ . Using the Heron-type formula for the volume of a tetrahedron found here with these side lengths we find that each tetrahedron has a volume of $\frac{3}{35}k^3$ , which makes the volume of the center dodecahedron $V_M = 24 \cdot \frac{3}{35}k^3 = \frac{72}{35}k^3$ .

Therefore, the ratio of the volumes is $\frac{V_M}{V} = \frac{\frac{72}{35}k^3}{72k^3} = \frac{1}{35}$ , and so $A = 1$ and $B = 35$ , and $A + B = 1 + 35 = \boxed{36}$ .

Wow! What a hard work! What I'm wondering is: if you chose 3 of the 12 plane equations to solve them, you would end up with (12 3)=220 diferent points I assume that you for example discard choseing two planes formed from two points on the same edge and there might be sistems without solution for example but there are stil too many points how do you chose the 14 of them you show here? Then there's another thing that I don't understand. Is not true that a dodecaedron has 20 verices? Can you please explain that.

Finaly at the last part when you talk about volumes shouldn't be k^3? And you could save time and space by developing the proof for k=1 and generalizing by similarity. Sorry that I'm always criticizing, it's not my intension.

Pau Cantos - 3 years, 3 months ago

Yes, not all the plane intersections are the vertices of the center dodecahedron, so some were discarded. Hopefully I can show which planes give which points, but that will take me a while to write out, so I'll reply with that later. The picture given in the problem was a big help for choosing the correct planes, though.

A dodecahedron is a polyhedron with $12$ flat faces, but can have a varying amount of edges and vertices. (You are probably thinking of a regular dodecahedron with $12$ pentagon faces and $20$ vertices.) This dodecahedron has $12$ kite faces so it has $\frac{12 \cdot 4}{2} = 24$ edges ( $12$ kites with $4$ edges each divided by $2$ faces sharing each edge). Then by Euler's polyhedron formula $V - E + F = 2$ we have $V - 24 + 12 = 2$ and so the number of vertices is $V = 14$ .

And yes, you are correct that the volumes should have a $k^3$ on them, not $k$ . Thanks for noticing! I edited my solution to fix that. I generally try to stay away from proving the general case of $k = 1$ in proofs because then it is hard to distinguish between varying exponents (for example, between $k$ , $k^2$ , and $k^3$ ).

David Vreken - 3 years, 3 months ago

The number of vertices can also be derived as follows : Notice that there are two types of vertices on the dodecahedron. Vertices with 3 edges connected to them and vertices with 4 edges. Each kite has exactly 2 vertices of each kind, therefore each participating for 1/3 or 1/4 of the total number of vertices. Since there are 12 kite faces, V = 12 ( 2 1/3 + 2*1/4) = 14

Dorian Subirana - 3 years, 2 months ago

$(-\frac{\sqrt{2}}{2}k, \frac{\sqrt{2}}{2}k, 0)$ is the intersection of $2\sqrt{2}x - \sqrt{2}y - 3z = -3k$ , $3\sqrt{2}y - z = 3k$ , and $\sqrt{2}x - 2\sqrt{2}y + 3z = -3k$

$(0, 0, k)$ is the intersection of $2\sqrt{2}x + \sqrt{2}y + 3z = 3k$ , $2\sqrt{2}x - \sqrt{2}y - 3z = -3k$ , and $2\sqrt{2}x + \sqrt{2}y - 3z = -3k$

$(\frac{\sqrt{2}}{2}k, \frac{\sqrt{2}}{2}k, 0)$ is the intersection of $3\sqrt{2}y - z = 3k$ , $2\sqrt{2}x + \sqrt{2}y + 3z = 3k$ , and $3\sqrt{2}x + z = 3k$

$(-\frac{\sqrt{2}}{2}k, -\frac{\sqrt{2}}{2}k, 0)$ is the intersection of $2\sqrt{2}x + \sqrt{2}y - 3z = -3k$ , $3\sqrt{2}x - z = -3k$ , and $\sqrt{2}x + 2\sqrt{2}y + 3z = -3k$

$(0, 0, -k)$ is the intersection of $\sqrt{2}x - 2\sqrt{2}y + 3z = -3k$ , $\sqrt{2}x + 2\sqrt{2}y - 3z = 3k$ , and $\sqrt{2}x - 2\sqrt{2}y - 3z = 3k$

$(\frac{\sqrt{2}}{2}k, -\frac{\sqrt{2}}{2}k, 0)$ is the intersection of $3\sqrt{2}x + z = 3k$ , $2\sqrt{2}x - \sqrt{2}y + 3z = 3k$ , and $3\sqrt{2}y + z = -3k$

$(-\frac{3\sqrt{2}}{7}k, 0, \frac{3}{7}k)$ is the intersection of $2\sqrt{2}x + \sqrt{2}y - 3z = -3k$ , $3\sqrt{2}x - z = -3k$ , and $2\sqrt{2}x - \sqrt{2}y - 3z = -3k$

$(0, \frac{3\sqrt{2}}{7}k, -\frac{3}{7}k)$ is the intersection of $\sqrt{2}x - 2\sqrt{2}y + 3z = -3k$ , $\sqrt{2}x + 2\sqrt{2}y - 3z = 3k$ , and $3\sqrt{2}y - z = 3k$

$(\frac{3\sqrt{2}}{7}k, 0, \frac{3}{7}k)$ is the intersection of $3\sqrt{2}x + z = 3k$ , $2\sqrt{2}x - \sqrt{2}y + 3z = 3k$ , and $2\sqrt{2}x + \sqrt{2}y + 3z = 3k$

$(-\frac{3\sqrt{2}}{5}k, 0, -\frac{3}{5}k)$ is the intersection of $3\sqrt{2}x - z = -3k$ , $\sqrt{2}x - 2\sqrt{2}y + 3z = -3k$ , and $\sqrt{2}x + 2\sqrt{2}y + 3z = -3k$

$(0, -\frac{3\sqrt{2}}{5}k, \frac{3}{5}k)$ is the intersection of $\sqrt{2}x + 2\sqrt{2}y - 3z = 3k$ , $3\sqrt{2}x + z = 3k$ , and $\sqrt{2}x - 2\sqrt{2}y - 3z = 3k$

$(\frac{3\sqrt{2}}{5}k, 0, -\frac{3}{5}k)$ is the intersection of $2\sqrt{2}x - \sqrt{2}y + 3z = 3k$ , $2\sqrt{2}x + \sqrt{2}y - 3z = -3k$ , and $3\sqrt{2}y + z = -3k$

$(0, \frac{3\sqrt{5}}{5}k, \frac{3}{5}k)$ is the intersection of $2\sqrt{2}x - \sqrt{2}y - 3z = -3k$ , $2\sqrt{2}x + \sqrt{2}y + 3z = 3k$ , and $3\sqrt{2}y - z = 3k$

$(0, -\frac{3\sqrt{2}}{7}k, -\frac{3}{7}k)$ is the intersection of $\sqrt{2}x - 2\sqrt{2}y - 3z = 3k$ , $\sqrt{2}x + 2\sqrt{2}y + 3z = -3k$ , and $3\sqrt{2}y + z = -3k$

David Vreken - 3 years, 3 months ago

Hosam Hajjir
Mar 8, 2018

My approach was all computerized. The steps in my solution were as follows:

Generate the equations of the 12 cutting planes.
Intersect these 12 planes, three at a time, thus generating all the possible intersection points.
Filter the points generated retaining only the points that have a non-negative projection with the normal to the 12 planes.
Generate a list (array) of the points belonging to each plane (face).
Order the points for each face in a counter clockwise direction.
Compute the area of the face and the distance from the center of the tetrahedron to the face.
Add the volumes of the all the pyramids having bases as the faces and apex at the center of the tetrahedron.
Divide the volume of the core by the volume of the tetrahedron, to find the required ratio.
The ratio turns out to be $\dfrac{1}{35}$ . Therefore, the answer is $36$ .

Could you give more details about 3? I don't understand exactly what are you cheking and why.

Pau Cantos - 3 years, 3 months ago

The points generated in step 2 do not necessarily lie on the edges of the intersection of all of the 12 planes. Step 3 guarantees that we take into consideration only the points that lie on the boundary of the intersection core ( shown rotating above).

Hosam Hajjir - 3 years, 3 months ago

Tanuel Chi
Mar 7, 2018

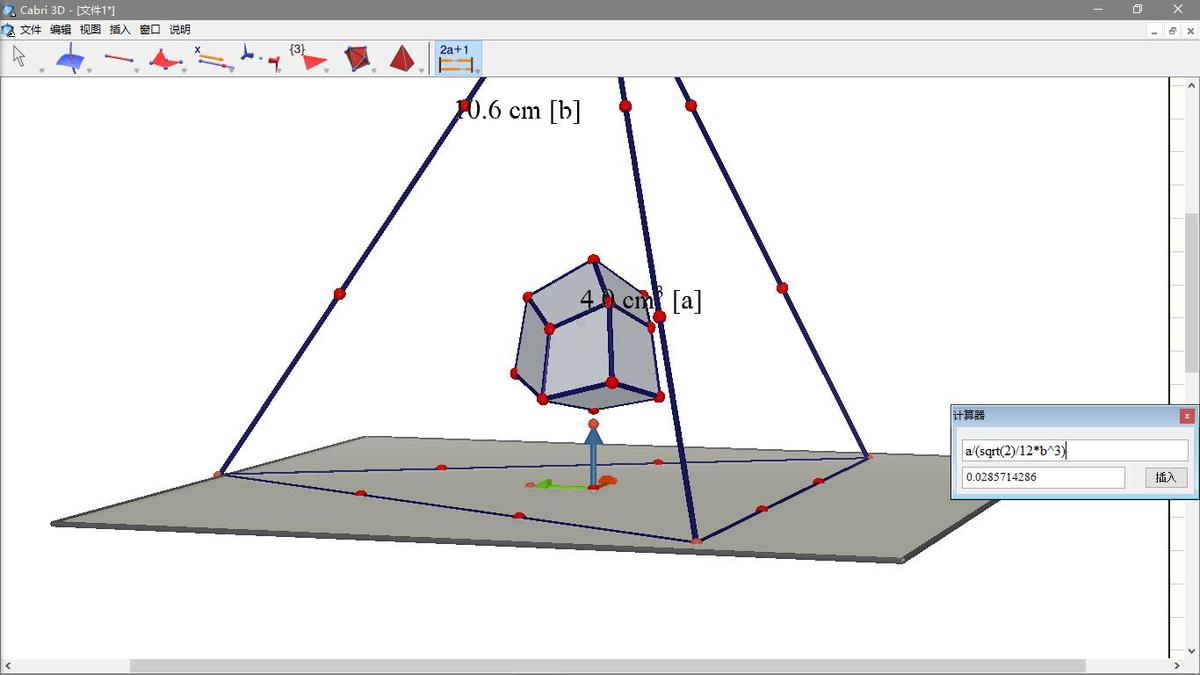I just can't get to a simple solution which don't need to compute all the intersection line and point, so I use the Cabri3D to draw answer.

3D Marion's Theorem

The answer is 36.

5 solutions

0 pending reports