3D Pendulum
A point mass m = 1 is attached to the free end of a mass-less rigid rod of length L = 1 . The other end of the rod is attached to the origin with a ball joint, allowing the free end to be positioned at an arbitrary point in 3 D space (constrained by the length of the rod, or course). The gravitational acceleration is 1 0 in the negative z direction.
Initially, the rod is rotating in the x y plane with angular speed ω = 7 (radians per second) with respect to the z axis. As the rod moves, what is the minimum z coordinate reached by its free end?
Bonus: Plot the trajectory
The answer is -0.357.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the pendulum be parameterized in spherical coordinates such that:
A = θ B = ϕ
Coordinates of the bob at an arbitrary instant are:
x = sin A cos B y = sin A sin B z = cos A
The kinetic energy and potential of the rod is:
T = 2 1 ( x ˙ 2 + y ˙ 2 + z ˙ 2 ) V = 1 0 cos A
Using the Lagrangian approach or the energy conservation principle, the equations of motion can be derived which are (working left out):
A ¨ = ( sin A cos A ) B ˙ 2 + 1 0 sin A B ¨ = − 2 B ˙ A ˙ cot A
Initial conditions are: A ( 0 ) = 2 π B ( 0 ) = 0 A ˙ ( 0 ) = 0 B ˙ ( 0 ) = 7
Numerical integration does the rest beyond this point. However, I am presenting an analytical approach similar to that of @Alak Bhattacharya as follows. Consider the second equation of motion
B ¨ = − 2 B ˙ A ˙ cot A ⟹ B ¨ = d t d B ˙ = d A d B ˙ d t d A = − 2 B ˙ A ˙ cot A ⟹ d A d B ˙ = − 2 B ˙ cot A
Separating variables and integrating gives:
ln B ˙ = − 2 ln ( sin A ) + ln K
Where K is an integration constant. SImplifying gives:
B ˙ = sin 2 A K
Applying initial condition yields that K = 7 . Thus:
B ˙ = sin 2 A 7
Using the above result in the first equation of motion:
A ¨ = ( sin A cos A ) B ˙ 2 + 1 0 sin A
⟹ A ˙ d A d A ˙ = sin A cos A ( sin 4 A 4 9 ) + 1 0 sin A ⟹ A ˙ d A ˙ = ( ( sin 3 A 4 9 cos A ) + 1 0 sin A ) d A
Integrating both sides again:
A ˙ 2 = − sin 2 A 4 9 − 2 0 cos A + C
Applying initial conditions again:
A ˙ 2 = − sin 2 A 4 9 − 2 0 cos A + 4 9
Finally, consider:
z = cos A
For z to be minimum:
z ˙ = − sin A A ˙ = 0
⟹ A ˙ = 0 ⟹ − sin 2 A 4 9 − 2 0 cos A + 4 9 = 0
This leads to a quadratic equation in cos A . Solving and realising that A > π / 2 since the bob moves downward results in:
cos A ≈ − 0 . 3 5 6 3
Hence the minimum Z-coordinate is:
z m i n = − 0 . 3 5 6 3
Missed the bit about the trajectory. Here it is:
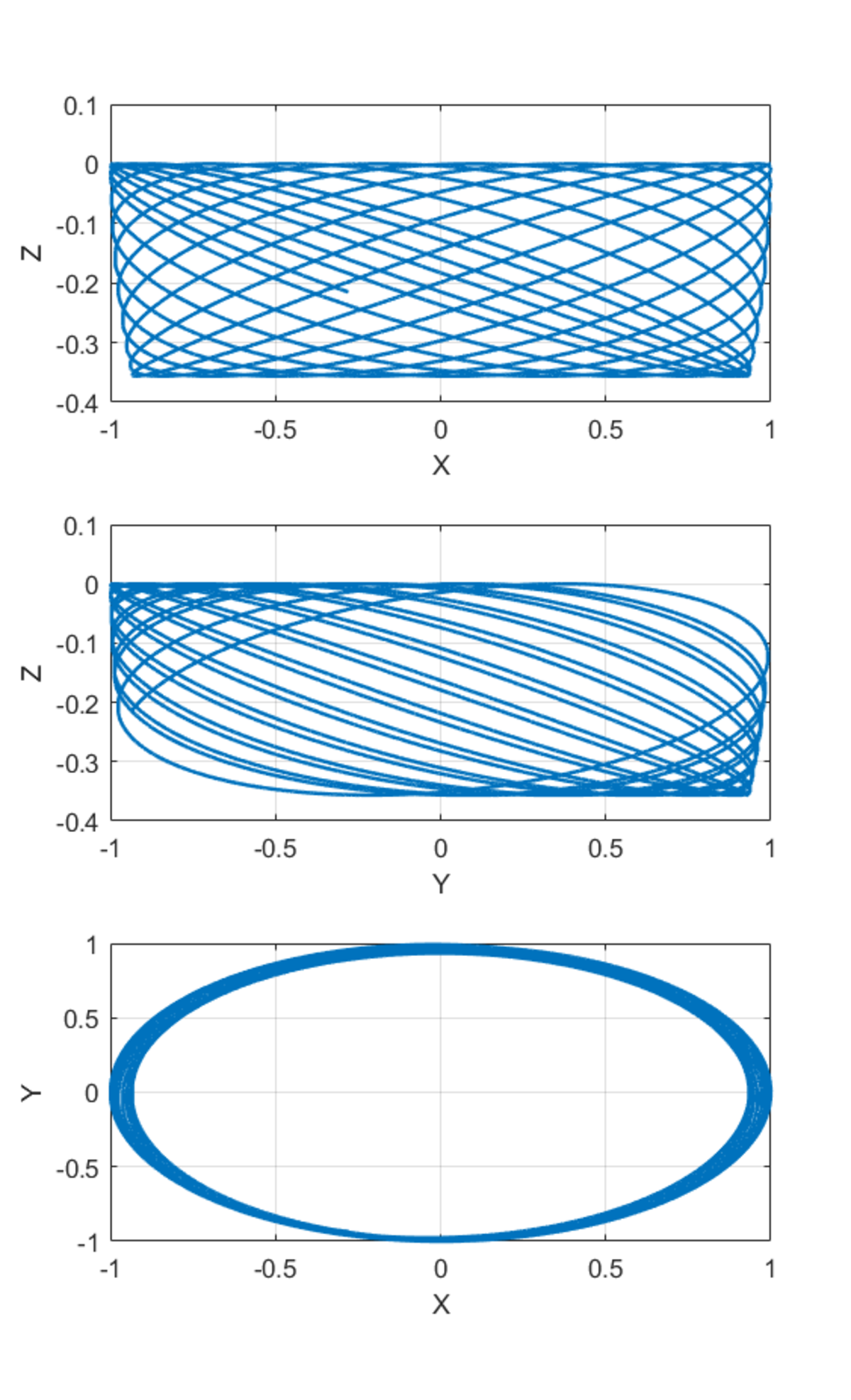
One can see the formation of an intricate pattern in 3D space. I have given three fundamental views here.
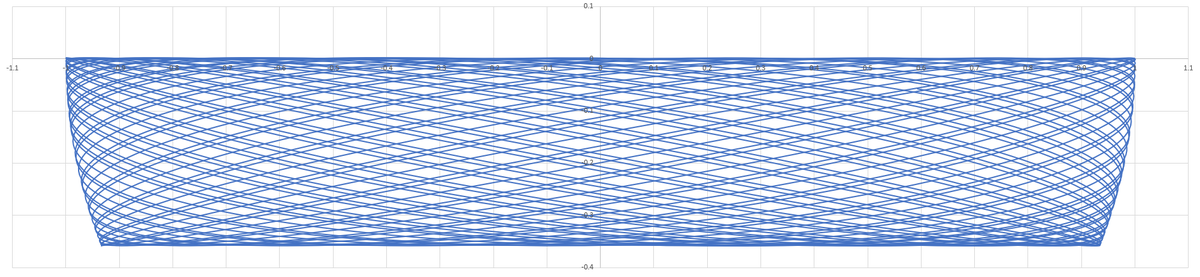
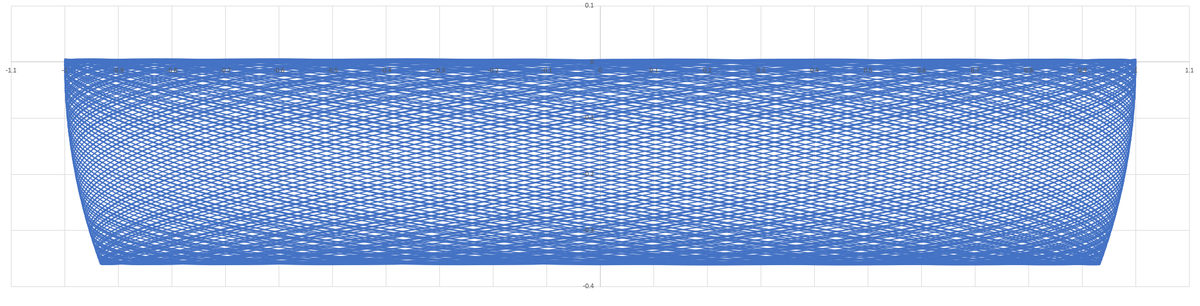
Thanks to @Alak Bhattacharya and @Karan Chatrath for the detailed solutions. I will simply add some plots of the trajectory in the x z plane. The plots are for 1 0 seconds, 3 0 seconds, and 1 0 0 seconds. The trajectory is essentially confined to a "band" on the surface of a sphere.

@Steven Chase Nice problem. Post more problems in pendulum
Log in to reply
@Steven Chase How can we parametrise ellipsoid and write its d A ??

Let at time t , the angle that the rod makes with vertical be α . Then the angular velocity of the point mass is given by ω = sin 2 α k , where k is a constant (since the line of centrifugal force intersects the z -axis and the line of weight force is parallel to that axis, the moments of both about that axis are zero).
Let β = d t d α . Then β d α d β = sin 3 α k 2 cos α − g sin α
⟹ β 2 = 2 g cos α − sin 2 α k 2 . Here I assumed that the rod was horizontal initially, so that k = 7 .
When α is minimum, β = 0 ⟹ 2 g sin 2 α = 4 9 cos α ⟹ cos α = 2 4 + ( 2 g 4 9 ) 2 − 2 g 4 9 ≈ 0 . 3 5 6 3 3 6 4 6 .
Hence the minimum z coordinate is − 0 . 3 5 6 3 .