4 arcs in a square
The figure below shows a unit square with four arcs drawn inside it. The centers of these arcs lie on the sides and are depicted by dots of the same color. The dots are 3 1 from one end of the side and 3 2 from the other end. The radius of each of the arcs is 3 2 . The intersection of the four arcs is a set of four points (depicted by four red dots). If we connect these four dots, they would form a tilted square. Find the tilt angle θ , 0 < θ < 4 5 ∘ , that this small square makes with the standard orientation of a square (the standard orientation is when its sides are parallel to the coordinate axes).
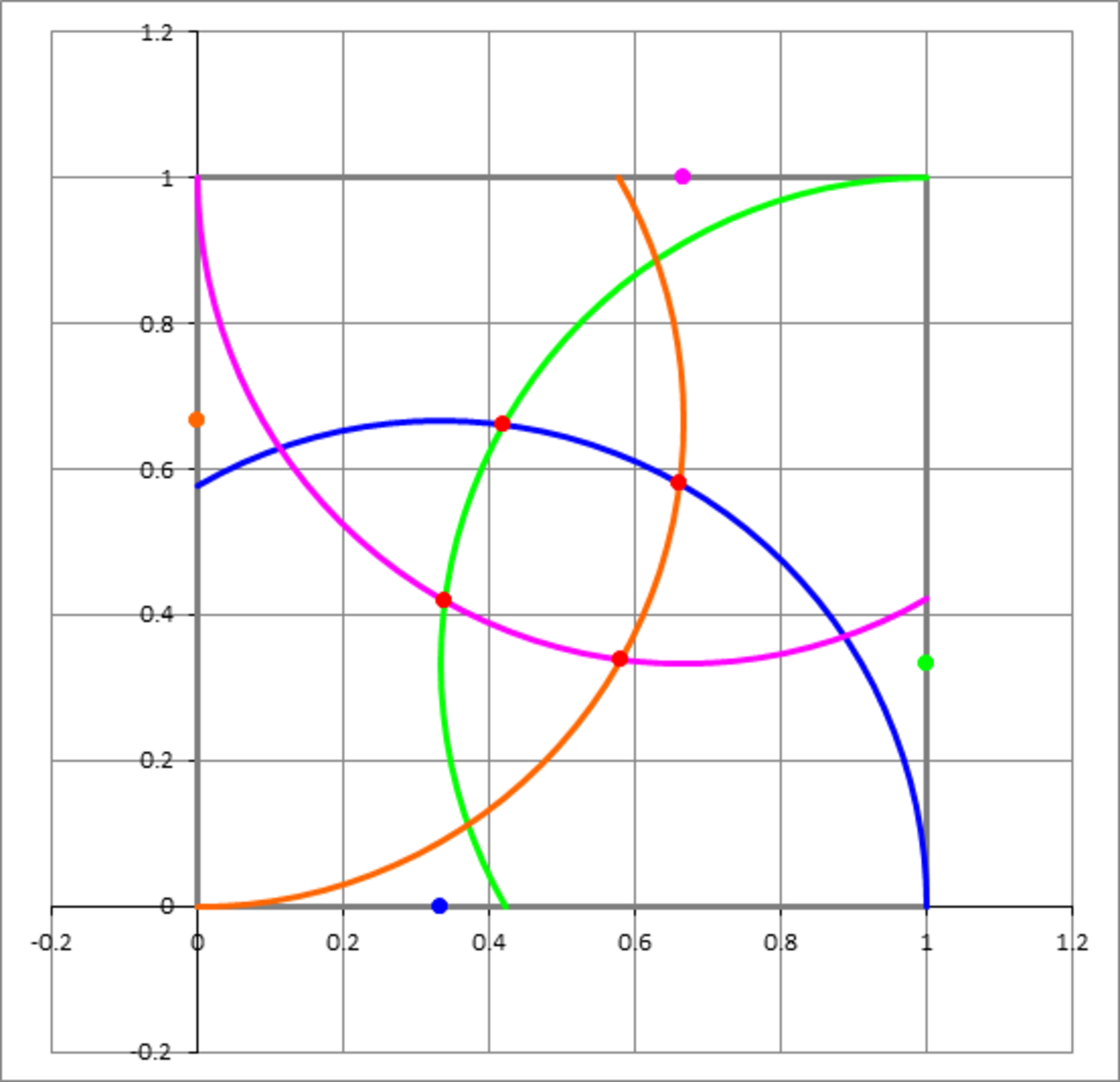
The answer is 18.43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
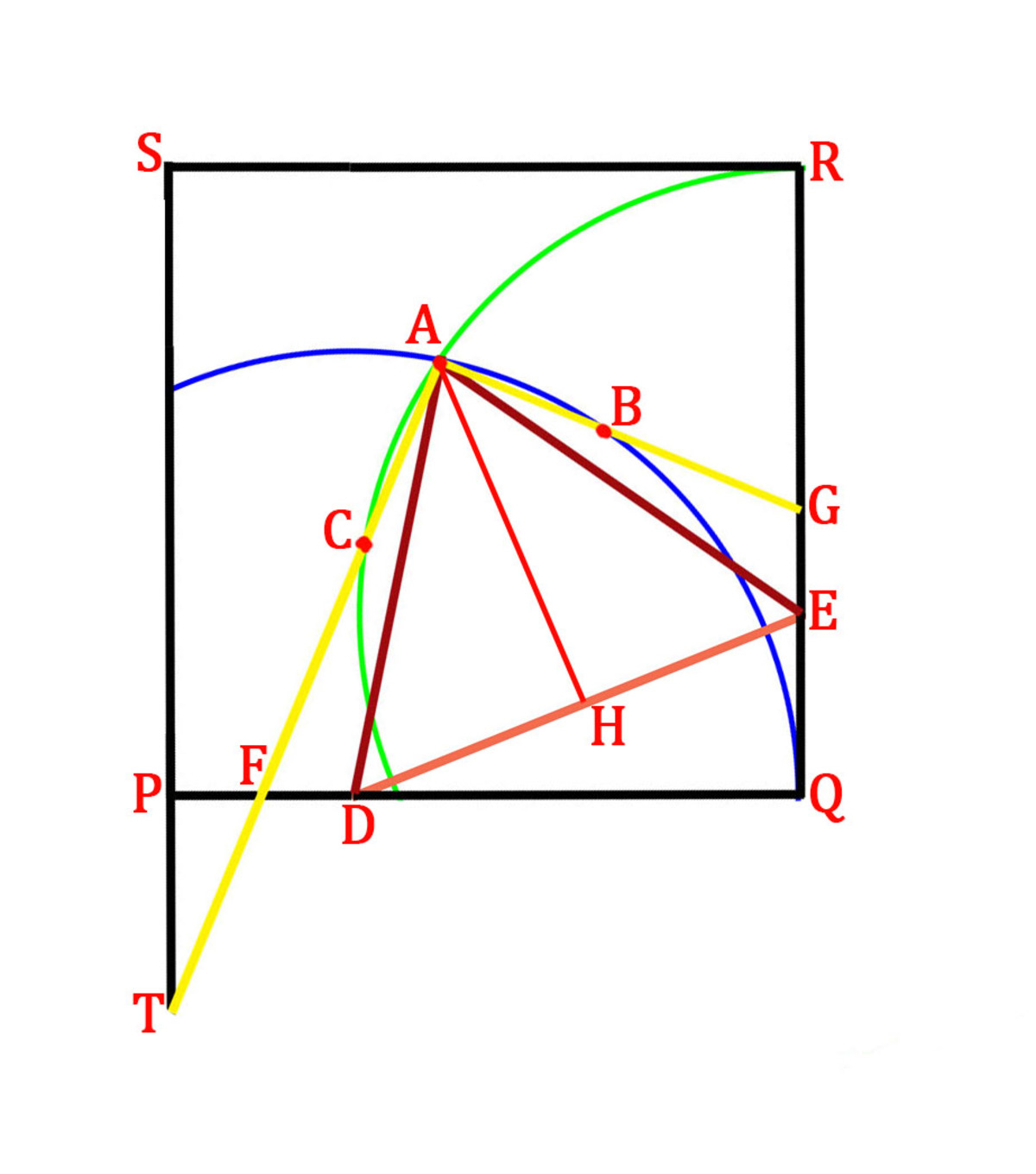 Let
D
and
E
be the center of blue and green circle respectively. These two circles intersect each other at
A
. Join
A
D
and
A
E
. Let
B
be the
intersection of blue and orange circle and
C
be the intersection of green and purple circle (see question figure).
Let
D
and
E
be the center of blue and green circle respectively. These two circles intersect each other at
A
. Join
A
D
and
A
E
. Let
B
be the
intersection of blue and orange circle and
C
be the intersection of green and purple circle (see question figure).
Join A B and A C and extend A C to intersect the sides of square P Q R S at F and T . We have to find ∠ A F D or ∠ P T F whichever is less than 45 ° .
D E = D Q 2 + Q E 2 = ( 3 2 ) 2 + ( 3 1 ) 2 = 3 5 A D = A E = radius of circles = 3 2 ⇒ △ A D E is isosceles. Draw A H perpendicular to D E . Then D H = H E . s i n ( ∠ D A H ) = c o s ( ∠ A D E ) = A D D H = 3 2 6 5 = 4 5 … Eq. 1 ⇒ c o s ( ∠ D A H ) = 4 1 1 … Eq. 2
If we remove the sides of large square and draw all the four circles, we will see that the figure will be symmetrical about line A H . ⇒ line C A is deflected from line D A by the same angle as line B A is deflected from line E A . ⇒ ∠ C A D = ∠ B A E … Eq. 3 Also, ∠ C A B = 9 0 ° as C A and A B are the sides of the tilted square. From the figure, ∠ C A B = ∠ C A D + ∠ D A E + ∠ B A E ⇒ ∠ C A B = 2 ( ∠ C A D ) + 2 ( ∠ D A H ) ⇒ ∠ C A D = 2 ∠ C A B − ∠ D A H = 4 5 ° − c o s − 1 ( 4 1 1 ) … Eq. 4
c o s ( ∠ E D Q ) = D E D Q = 5 / 3 2 / 3 = 5 2 … Eq. 5
We know that in a triangle, exterior angle is equal to the sum of opposite interior angles. Applying this to △ A F D , ∠ A D Q = ∠ A F D + ∠ F A D ⇒ ∠ A F D = ∠ A D Q − ∠ F A D = ∠ A D E + ∠ E D Q − ∠ F A D Using Eq. 1, 4 and 5 ∠ A F D = c o s − 1 ( 4 5 ) + c o s − 1 ( 5 2 ) − ( 4 5 ° − c o s − 1 ( 4 1 1 ) )
⇒ ∠ A F D = c o s − 1 ( 4 5 2 5 − 1 1 ) − c o s − 1 ( 4 2 5 + 1 1 ) = c o s − 1 ( 1 0 1 ) > c o s − 1 ( 2 1 ) = 4 5 °
∠ P F T = ∠ A F D = c o s − 1 ( 1 0 1 ) [ Vertically opposite angles ]
∠ P T F = 9 0 ° − ∠ P F T = 9 0 ° − c o s − 1 ( 1 0 1 ) = s i n − 1 ( 1 0 1 ) = 1 8 . 4 3 °
The blue arc has equation ( x − 3 1 ) 2 + y 2 = 9 4 .
The green arc has equation ( x − 1 ) 2 + ( y − 3 1 ) 2 = 9 4 .
Solving these simultaneously, we find the two arcs meet at the point ( u , v ) = ( 3 0 1 ( 2 0 − 5 5 ) , 3 0 1 ( 5 + 2 5 5 ) ) . (Note there is a second solution outside the square which we discard.)
By symmetry, the orange and blue arcs meet at the point ( v , 1 − u ) . It's now simple coordinate geometry to calculate the gradient of the line joining these points, and hence the tilt angle of 1 8 . 4 3 ∘ .
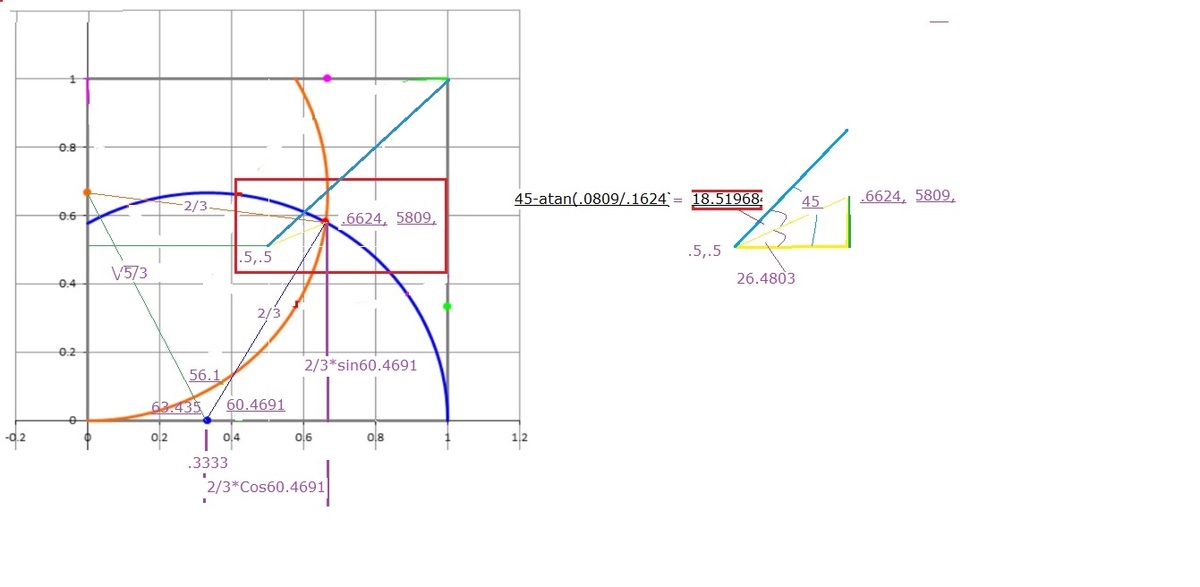
Taking the parametric equation of the blue arc
r 1 ( t ) = 3 1 ( 1 + 2 cos t , 2 sin t ) , where 0 ≤ t ≤ cos − 1 ( 2 − 1 )
while the green arc is given by
r 2 ( s ) = 3 1 ( 3 − 2 sin s , 1 + 2 cos s ) , where 0 ≤ s ≤ cos − 1 ( 2 − 1 )
To find the intersection point, we equate the vectors r 1 ( t ) and r 2 ( s ) .
This results in the system of equations,
1 + 2 cos t = 3 − 2 sin s
2 sin t = 1 + 2 cos s
Squaring and adding, yields
1 + 4 + 4 cos t = 9 + 1 + 4 − 1 2 sin s + 4 cos s
From which,
cos t = 4 9 − 3 sin s + cos s
Plugging this into the first equation,
1 + 2 9 − 6 sin s + 2 cos s = 3 − 2 sin s
So that,
2 cos s − 4 sin s = − 2 5
which becomes, after dividing through by 2,
cos s − 2 sin s = − 4 5
This equation can solved for an exact value of s , as follows:
The left hand side can be written as
5 cos ( s + ϕ ) = − 4 5
where ϕ = tan − 1 ( 2 )
And hence the two solutions of the equation are,
s 1 = − ϕ + cos − 1 ( − 4 5 ) = 6 0 . 5 5 2 9 ∘
and
s 2 = 3 6 0 ∘ − s 1 = 2 9 9 . 4 4 7 1 ∘
The valid solution here is s 1 , hence the point of intersection is
r 2 ( s 1 ) = 3 1 ( 3 − 2 sin s , 1 + 2 cos s ) = ( 0 . 4 1 9 4 6 , 0 . 6 6 1 1 )
The ray connecting the center of the square to the above point is
v = r 2 ( s 1 ) − ( 0 . 5 , 0 . 5 ) = ( − 0 . 0 8 0 5 4 , 0 . 1 6 1 1 )
Now, the tilt angle is
θ = 1 3 5 ∘ − atan2 ( − 0 . 0 8 0 5 4 , 0 . 1 6 1 1 ) = 1 3 5 ∘ − 1 1 6 . 5 6 2 2 ∘ = 1 8 . 4 3 ∘
By symmetry, the line through the orange and green point will be parallel to one of the sides of the tilted square.
Since a line through ( 0 , 3 2 ) and ( 1 , 3 1 ) has a slope of − 3 1 , the angle is ∣ tan − 1 − 3 1 ∣ ≈ 1 8 . 4 3 ° .