$4$ BUGS

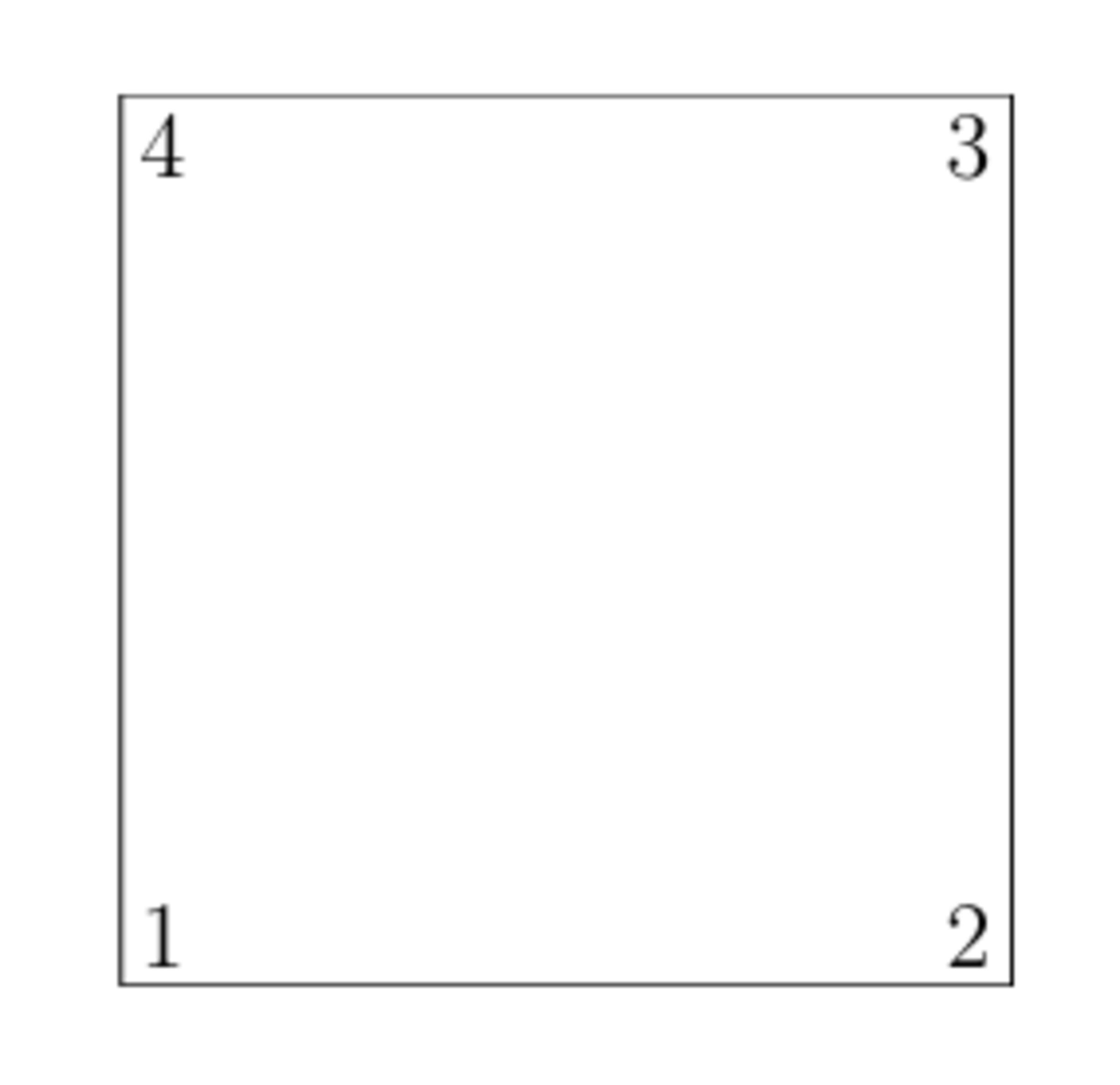
$4$ bugs are placed on $4$ square vertices ,

Where the bug number $i$ is placed on vertix number $i.$

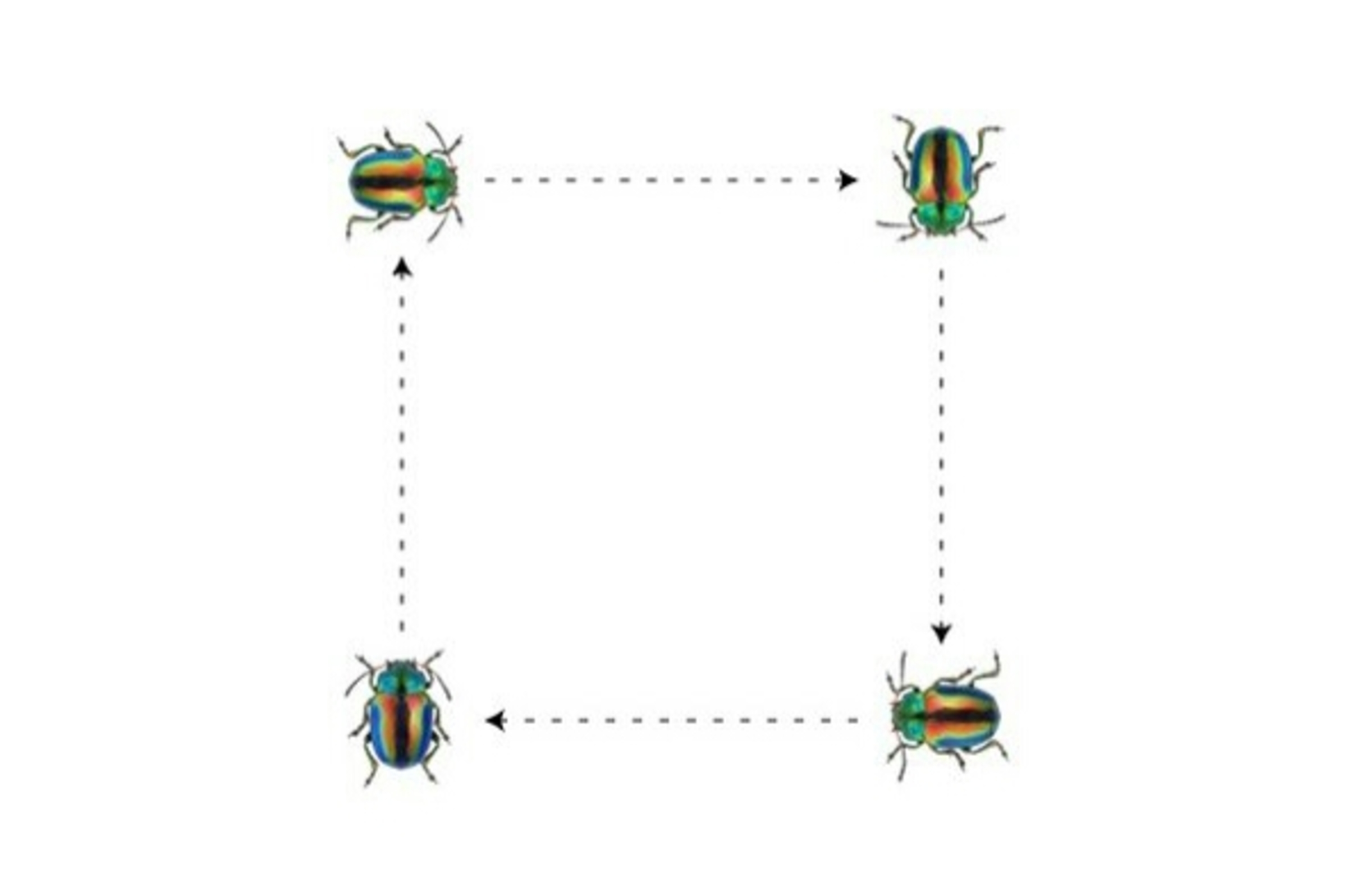
If the day is $\left\{sunday,wednesday,friday\right\}$ , the bugs will go cloclwise such that the bug number $1$ will go one step , the bug number $2$ will go two steps , the bug number $3$ will go four steps , the bug $4$ will not move.

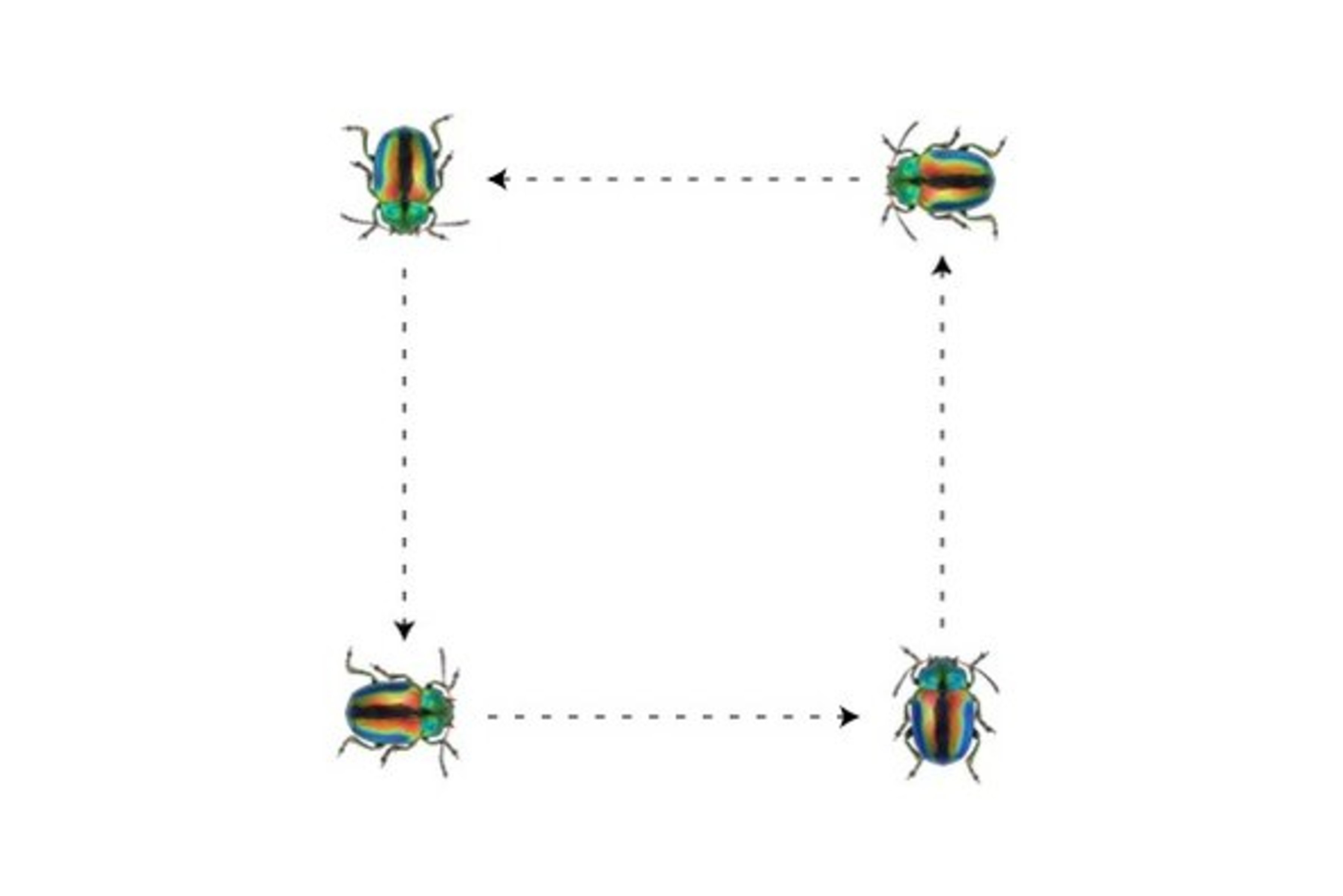
If the day is $\left\{monday,tuesday,saturday\right\}$ , the bugs will go counterclockwise such that the bug number $1$ will go four steps , the bug number $2$ will go three steps , the bug number $3$ will go five steps , the bug $4$ will not move

If the day is $\left\{thursday\right\}$ , the bugs $1,4$ will not move , the bugs $2,3$ will go $2$ steps clockwise .

Today is sunday , and the bugs didn't start moving yet

step is the length of one side of the square

In which day of the week "at the end of the day" will the four bugs be on the same vertix for the first time ?