4 Circles in a Triangle
A right triangle is divided into two smaller triangles by the altitude of its hypotenuse. An incircle is inscribed in the upper triangle, while the lower triangle contains three circles which are tangent with each other as well as the sides of the lower triangle, as shown in the figure. All four circles are congruent. What is the ratio of the area of the four circles to the area of the original right triangle? If this ratio can be expressed as where are squarefree and coprime, then submit .
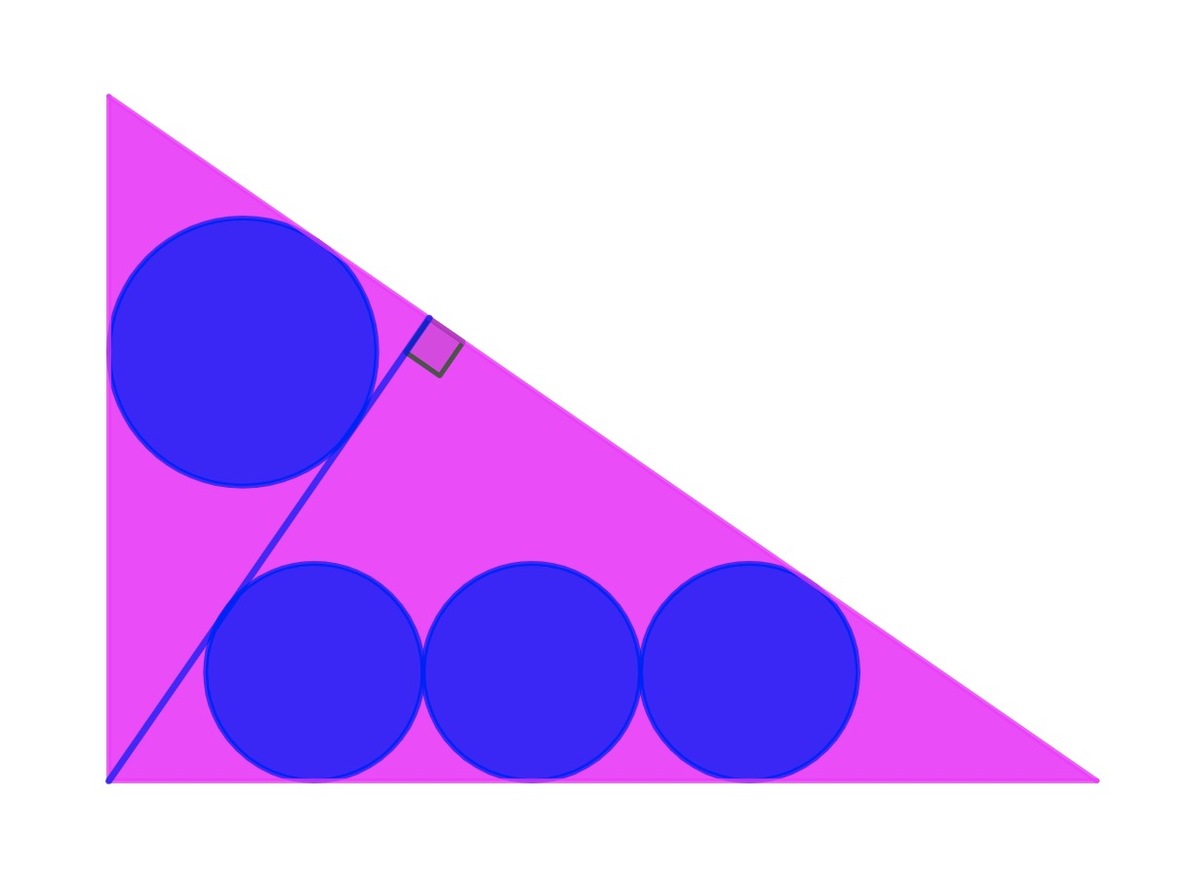
Note: The diagram is not drawn to scale.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice problem!
Fun fact: it is a 3 0 ∘ - 6 0 ∘ - 9 0 ∘ triangle.
Referring to the figure above, △ A B D and △ C M F are similar. Their similarity ratio is equal to the ratio of their inradii, which is 1 , hence the triangles are congruent.
Let A B = c , A C = b , ∠ A B C = B , ∠ A C B = C , cot 2 B = x . Denote the radius of each one of the four circles by r .
2 B + 2 C = 4 π ⇒ cot ( 2 B + 2 C ) = 1 ⇒ x + cot 2 C x cot 2 C − 1 = 1 ⇒ cot 2 C = x − 1 x + 1 Since △ A B D and △ C M F are congruent, A D = F C ⇒ c ⋅ sin B = r cot 2 C + r ⇒ c ⋅ cot 2 2 B + 1 2 cot 2 B = r cot 2 C + r ⇒ c ⋅ x 2 + 1 2 x = r ( x − 1 x + 1 + 1 ) ⇒ c = r ⋅ x − 1 x 2 + 1 ( 1 ) Moreover, b = A E + E G + G C = r cot 2 B + 4 r + r cot 2 C = r ( x + 4 + x − 1 x + 1 ) = r ⋅ x − 1 x 2 + 4 x − 3 ( 2 ) These results yield a restriction for x : b > 0 c > 0 } ⇒ x − 1 x 2 + 4 x − 3 > 0 x > 1 ⎭ ⎪ ⎬ ⎪ ⎫ ⇒ x > 1 ( 3 ) Now we proceed to an equation for finding x cot B = b c ⇔ 2 cot 2 B cot 2 2 B − 1 = b c ⇔ 2 x x 2 − 1 = r ⋅ x − 1 x 2 + 4 x − 3 r ⋅ x − 1 x 2 + 1 which simplifies to x 4 + 2 x 3 − 4 x 2 − 6 x + 3 = 0 ⇔ ( x 2 − 3 ) ( x 2 + 2 x − 1 ) = 0 ⇔ x = ± 3 o r x = − 1 + 2 o r x = − 1 − 2 Due to the restriction ( 3 ) , the only accepted solution is x = 3 .
Finally, we go for the required ratio:
( 1 ) , ( 2 ) ⇒ b c = ( r x − 1 x 2 + 4 x − 3 ) ⋅ ( r x − 1 x 2 + 1 ) ⇒ x = 3 b c = 8 r 2 ( 2 3 + 3 ) ⇒ b c r 2 = 2 4 2 3 − 3 Hence, r a t i o = 2 1 b c 4 π r 2 = 8 π ⋅ 2 4 2 3 − 3 = π ( 3 2 3 − 1 ) . For the answer, a = 2 , b = 3 , c = 1 , thus a + b + c = 6 .
PS: x = 3 ⇒ cot 2 B = 3 ⇒ 2 B = 3 0 ∘ ⇒ B = 6 0 ∘ . △ A B C is indeed a 3 0 ∘ - 6 0 ∘ - 9 0 ∘ triangle.