4 Circles in space - general case
Four circles have radii of 4 1 , 4 0 , 3 5 and 3 0 . You want to arrange them in 3D space, such that each of the circles is tangent to the other three. So first you lay the circle with radius 4 1 on the floor so that its plane is the horizontal x y plane. Next you place the following circles one after the other such that each one is tangent to the big circle on the floor and to the previous circle that you added. At the end each of the four circles is tangent to the other three.
After you do this, how high ( z -coordinate) will the tangency point between the circle with radius 4 0 and the circle with radius 3 5 be above the x y plane ? (This is point A is the attached figure).
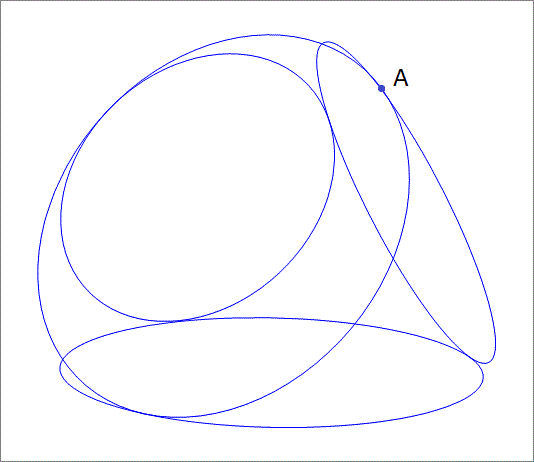
The answer is 59.283.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
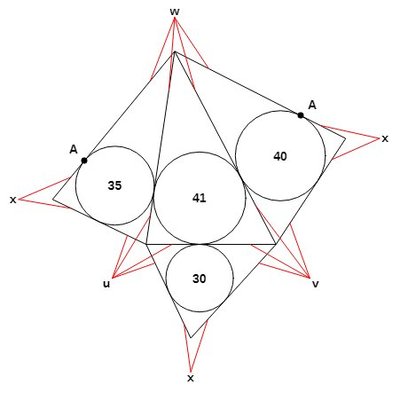
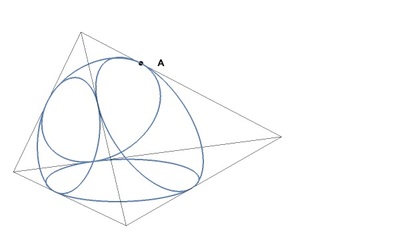We need to find a tetrahedron, whose faces have incircles of radii
4
1
,
4
0
,
3
5
,
3
0
, where the various incircles meet each other at their points of tangency with the edges of the tetrahedron. This means that the various sides of the tetrahedron will have lengths
u
v
,
u
+
w
,
u
+
x
,
v
+
w
,
v
+
x
,
w
+
x
where
u
,
v
,
w
,
x
are the distances of the points of tangency of the incircles to the vertices of the tetrahedron, as shown in the net of the tetrahedron below. Applying Heron's formula to each of the faces of the tetrahedron tells us that
4
1
3
5
=
=
u
+
v
+
w
u
v
w
u
+
w
+
x
u
w
x
4
0
3
0
=
=
v
+
w
+
x
v
w
x
u
+
v
+
x
u
v
x
These equations can be solved numerically to obtain the solutions
u
=
4
7
.
5
0
8
,
v
=
6
7
.
8
3
9
9
,
w
=
1
2
5
.
7
5
,
x
=
4
4
.
6
9
0
4
, and it is now simply a matter of determining the height of the top vertex of the tetrahedron above the base. We can show that the base can have coordinates
(
0
,
0
)
,
(
1
1
5
.
3
4
8
,
0
,
0
)
and
(
2
5
.
3
4
2
6
,
1
7
1
.
3
9
5
,
0
)
, while the top vertex has coordinates
(
3
9
.
6
3
0
7
,
2
1
.
7
6
3
4
,
8
0
.
3
5
1
2
)
. Thus the height of the top vertex above the base is
8
0
.
3
5
1
2
, and so the height of the point
A
above the base is
x
+
w
w
×
8
0
.
3
5
1
2
=
5
9
.
2
8
2
7
In order for four circles to be tangent to each other, the tetrahedron edge lengths have to meet the criteria: a + a' = b + b'=c + c'
where a' is an edge opposite to a (Crelle's tetrahedron).
Log in to reply
In my notation, that just says that u + v + w + x can be obtained by summing the four terms in three different sets of pairs, namely ( u + v ) + ( w + x ) = ( u + w ) + ( v + x ) = ( u + x ) + ( v + w ) .
I just added an extra info about Crelle's tetrahedron. I am sure the property did come up in your solution.