4 Circles in space
Three circles of radius 5 0 and one big circle of radius 7 0 are to be arranged such that the big circle lies in the horizontal x y plane (the ground) and each of the three smaller circles, are tangent to the big circle and tangent to the other two small circles.
How high above the ground is the tangency point between two small circles? (these are points A, B, and C in the attached figure)
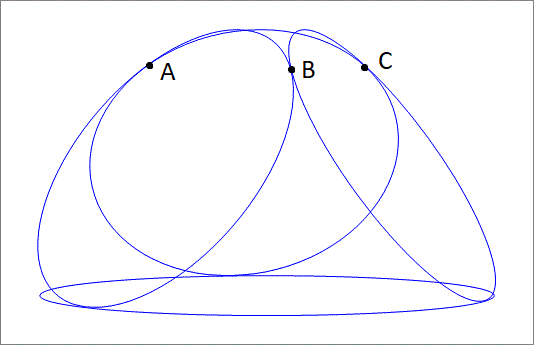
The answer is 69.56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
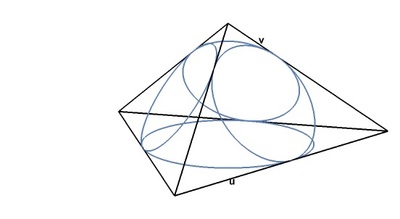 The four circles will be the incircles of a triangular pyramid with equilateral triangle base, and with three congruent isosceles triangles as the other three sides. The incircle of the base will have radius
7
0
, while the inradius of the isosceles triangles will be
5
0
. The incircles will touch each other at their points of tangency with the edges of the tetrahedron. Thus the equilateral triangle base will have sides
2
u
, and the isosceles triangles will have sides of length
2
u
,
u
+
v
,
u
+
v
, where
u
,
v
are the distances from the vertices of the triangular faces to the points of tangency with the incircles, as shown below.
The four circles will be the incircles of a triangular pyramid with equilateral triangle base, and with three congruent isosceles triangles as the other three sides. The incircle of the base will have radius
7
0
, while the inradius of the isosceles triangles will be
5
0
. The incircles will touch each other at their points of tangency with the edges of the tetrahedron. Thus the equilateral triangle base will have sides
2
u
, and the isosceles triangles will have sides of length
2
u
,
u
+
v
,
u
+
v
, where
u
,
v
are the distances from the vertices of the triangular faces to the points of tangency with the incircles, as shown below.
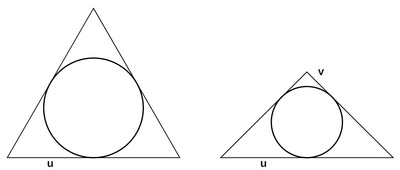 Since the equilateral triangle with side length
2
u
has inradius
7
0
, we deduce that
u
=
7
0
3
. Using Heron's formula, the isosceles triangle has area
u
2
v
(
2
u
+
v
)
. and hence has inradius
2
u
+
v
u
2
v
Since this equals
5
0
, we deduce that
v
=
6
1
1
7
5
0
3
. The height of
A
,
B
,
C
above the base is then equal to
u
+
v
u
times the height of the pyramid, and so is equal to
(
u
+
v
)
2
−
3
4
u
2
×
u
+
v
u
=
4
3
7
0
1
8
2
6
=
6
9
.
5
6
3
3
Since the equilateral triangle with side length
2
u
has inradius
7
0
, we deduce that
u
=
7
0
3
. Using Heron's formula, the isosceles triangle has area
u
2
v
(
2
u
+
v
)
. and hence has inradius
2
u
+
v
u
2
v
Since this equals
5
0
, we deduce that
v
=
6
1
1
7
5
0
3
. The height of
A
,
B
,
C
above the base is then equal to
u
+
v
u
times the height of the pyramid, and so is equal to
(
u
+
v
)
2
−
3
4
u
2
×
u
+
v
u
=
4
3
7
0
1
8
2
6
=
6
9
.
5
6
3
3
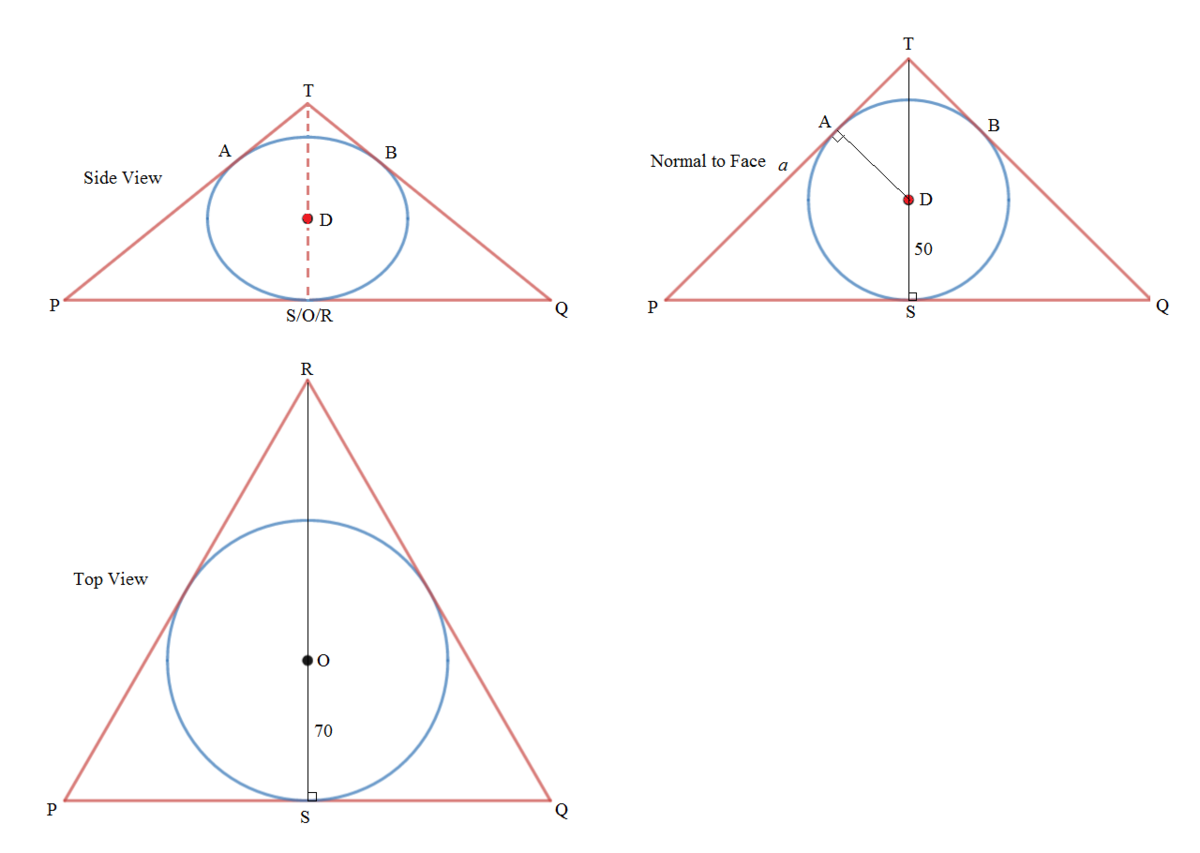
We notice that each of the four circles is on a face of a tetrahedron. Every circle is inscribed in the respective triangle and is internally tangent to the three sides of the triangle or the edges of the tetrahedron.
The base of the tetrahedron is an equilateral triangle P Q R inscribing a circle of radius 7 0 and center O (top view). S is where the circle tangent to P Q . Since O is the centroid of △ P Q R , R S = 3 O S = 2 1 0 and the side length of △ P Q R , P R = R S csc 6 0 ∘ = 1 4 0 3 .
The slanting faces of the tetrahedron are isosceles triangles congruent to △ P Q T with P T = Q T and P Q = 1 4 0 3 (normal to face view). △ P Q T has an incircle of radius 5 0 and center D , which is tangent to its sides at A , B , and S . Let P T = Q T = a . Then the semi-perimeter of △ P Q T , s = 2 2 a + 1 4 0 3 = a + 7 0 3 , and area of △ P Q T is s × inradius or [ P Q T ] = 5 0 s and by Heron's formula , we have [ P Q T ] = s ( s − a ) 2 ( s − 1 4 0 3 ) . Then we have,
( a + 7 0 3 ) ( 7 0 3 ) 2 ( a − 7 0 3 ) 7 0 3 ( a + 7 0 3 ) ( a − 7 0 3 ) a + 7 0 3 a − 7 0 3 a + 7 0 3 a − 7 0 3 ( 1 4 7 − 2 5 ) a ⟹ a = 5 0 ( a + 7 0 3 ) = 5 0 ( a + 7 0 3 ) = 7 3 5 = 1 4 7 2 5 = ( 1 4 7 + 2 5 ) 7 0 3 = 6 1 6 0 2 0 3
By Pythagorean theorem , T S = P T 2 − P S 2 = 6 1 2 6 0 2 0 2 ⋅ 3 − 7 0 2 ⋅ 3 = 6 1 7 3 5 0 . Since △ P S T and △ A D T are similar, then A D A T = P S T S ⟹ A T = P S T S ⋅ A D = 6 1 ⋅ 7 0 3 7 3 5 0 ⋅ 5 0 = 6 1 1 7 5 0 3 .
Now the height of the tetrahedron O T = T S 2 − O S 2 = 6 1 2 7 3 5 0 2 − 7 0 2 = 6 1 1 4 0 1 8 2 6 . The height of points A , B , and C above ground:
h = P T A P ⋅ O T = P T P T − A T ⋅ O T = ( 1 − P T A T ) O T = ( 1 − 6 0 2 0 1 7 5 0 ) 6 1 1 4 0 1 8 2 6 = 4 3 7 0 1 8 2 6 ≈ 6 9 . 5 6