4 Colored Square II
A square is partitioned into 4 colored triangles, as shown in the diagram. The blue, inscribed triangle has an area of 41, while the other three have distinct integer areas. The combined area of any two of these three triangles is always smaller than the area of the blue triangle.
If the square has area 96, what is the area of the smallest triangle?
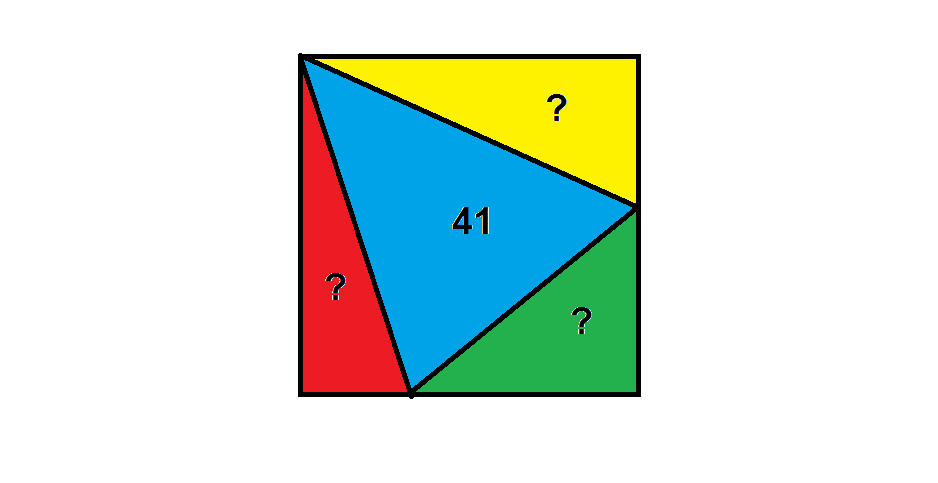
Inspired by 4 Colored Square
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Thanks to @Anton Wu in 4 Colored Square , we have a formula for computing the areas of the 4 triangles constructed within a square, where a < b < c stand for the areas of the triangles with square edges as their sides and d is the area of the inscribed triangle (blue one in this case):
d 2 = ( a + b + c ) 2 − 4 a c
From the question, we know that d = 4 1 and 9 6 = a + b + c + d . Thus, a + b + c = 9 6 − d = 9 6 − 4 1 = 5 5 .
Plugging in the values, we will obtain:
4 1 2 = 5 5 2 − 4 a c
5 5 2 − 4 1 2 = ( 5 5 − 4 1 ) ( 5 5 + 4 1 ) = 4 a c
a c = 1 4 × 2 4 = 1 6 × 2 1 = 1 2 × 2 8
Note that these are the only three possible combinations for a , c because, for example, if a = 8 and c = 4 , b = 5 5 − 4 2 − 8 = 5 , which is not correlated with a < b < c constraint.
Then for ( a , b , c ) is ( 1 4 , 1 7 , 2 4 ) , b + c = 4 1 , but the combination area must be less than 4 1 (the blue area exceeds any combination). Thus, this is not the desired solution.
For ( a , b , c ) is ( 1 6 , 1 8 , 2 1 ) , b + c = 3 9 , so any combination will be less than 4 1 .
Finally, for ( a , b , c ) is ( 1 2 , 1 5 , 2 8 ) , b + c = 4 3 , which exceeds the blue area and so is not satisfying the constraint.
Thus, a = 1 6 ; b = 1 8 ; c = 2 1 ; and d = 4 1 . As a result, the smallest triangle’s area is a = 1 6 .