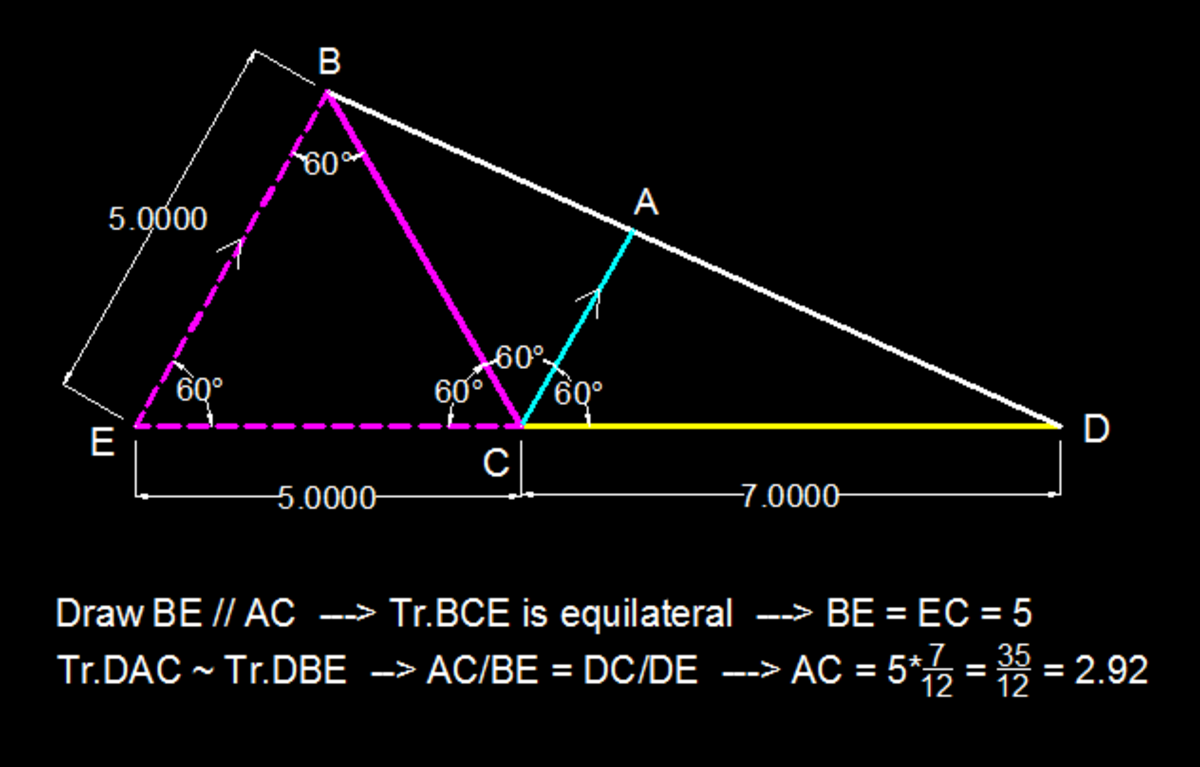
4 coplanar points
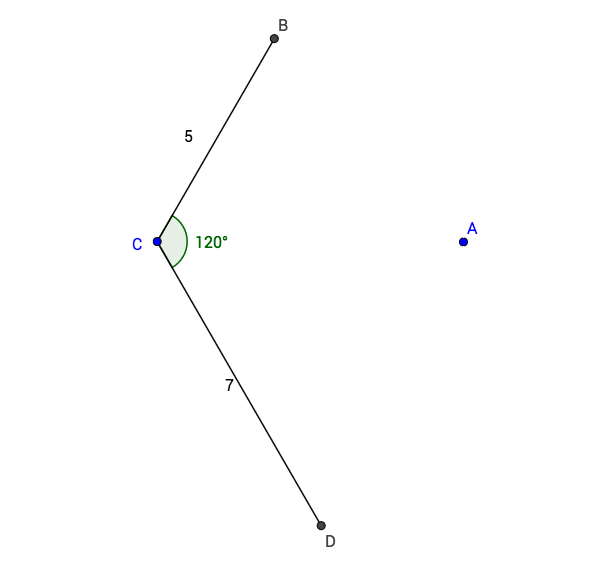
Let there exist 3 coplanar points B , C , and D such that B C = 5 and C D = 7 and ∠ B C D = 1 2 0 ∘ . A is a point in the same plane that lies on the angle bisector of ∠ B C D . Then what should be the value of C A so that the points B , A and D are collinear?
The answer is 2.92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
 .
.
We put the points in a coordinate system such that
C = ( 0 , 0 ) D = ( 7 , 0 ) B = ( 5 ⋅ cos 1 2 0 ° , 5 ⋅ sin 1 2 0 ° ) = ( − 2 5 , 2 5 3 )
And A lies on the line r : y = x ⋅ tan 6 0 ° = x 3
We now need only to find the intersection between r and B D
The line that passes through B D is
y = − 2 5 − 7 2 5 3 − 0 ( x − 7 ) = − 1 9 5 3 ( x − 7 )
To find the intersection
x 3 = − 1 9 5 3 ( x − 7 ) ⟺ x = 2 4 3 5 ⟹ y = 2 4 3 5 3
Therefore the lenght of A C is
A C = ( 2 4 3 5 ) 2 + ( 2 4 3 5 3 ) 2 = 1 2 3 5 ≈ 2 . 9 2
Consider the triangles B C A , A C D and B C D
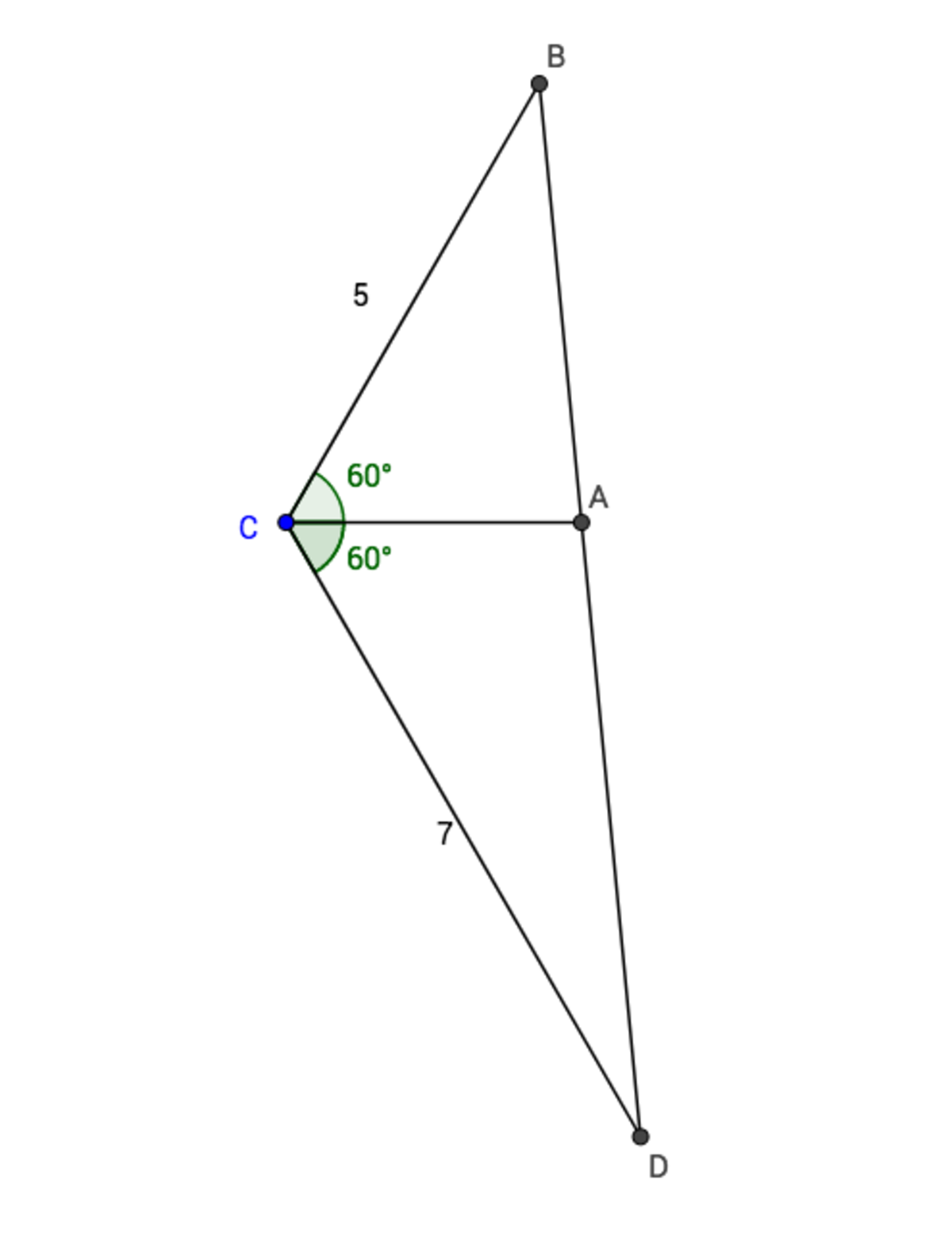
Now, we use the fact that if in a △ X Y Z if X Y = z , Y Z = x and Z X = y and ∠ X Y Z = 6 0 0 , then y 2 = x 2 + z 2 − 2 x z c o s 6 0 0 = x 2 + z 2 − x z
Thus, we get that if C A = a , then
B A 2 = 5 2 + a 2 − 5 a and D A 2 = 7 2 + a 2 − 7 a
By △ B C D , B D 2 = 5 2 + 7 2 − 2 ( 5 ) ( 7 ) c o s 1 2 0 o = 5 2 + 7 2 + 3 5
Now, A lies on BD if and only if B A + A D = B D
i.e. 5 2 + a 2 − 5 a + 7 2 + a 2 − 7 a = 5 2 + 7 2 + 3 5 ⟹ ( 5 2 + a 2 − 5 a ) + ( 7 2 + a 2 − 7 a ) + 2 ( 5 2 + a 2 − 5 a ) ( 7 2 + a 2 − 7 a ) = 5 2 + 7 2 + 3 5
⟹ ( − 2 a 2 + 1 2 a + 3 5 ) 2 = 4 ( 5 2 + a 2 − 5 a ) ( 7 2 + a 2 − 7 a )
⟹ 4 a 4 − 4 8 a 3 + 4 a 2 + 8 4 0 a + 1 2 2 5 = 4 a 4 − 4 8 a 3 + 4 3 6 a 2 − 1 6 8 0 a + 4 9 0 0
⟹ − 4 3 2 a 2 + 2 5 2 0 a − 3 6 7 5 = 0
⟹ a = 1 2 3 5
Thus,
C A = 2 . 9 2