4 Easy Circles, Part 2

Draw altitude $CG$ . Since the $13$ - $14$ - $15$ triangle is a $9$ - $12$ - $15$ right triangle combined with a $5$ - $12$ - $13$ right triangle at side $12$ , $CG = 12$ .

Now $\triangle AGC \sim \triangle AED$ and $\triangle BGC \sim \triangle BFD$ by AA similarity, so let $AE = 3m$ , $ED = 4m$ , $AD = 5m$ , and $r_{\triangle AED} = m$ (because it is similar to a $9$ - $12$ - $15$ or $3$ - $4$ - $5$ triangle, which has an inradius of $r = \frac{1}{2}(3 + 4 - 5) = 1$ ) and let $BF = 5n$ , $DF = 12n$ , $DB = 13n$ , and $r_{\triangle BFD} = 2n$ (because it is similar to a $5$ - $12$ - $13$ triangle, which has an inradius of $r = \frac{1}{2}(5 + 12 - 13) = 2$ ).

From segment addition, $AB = AD + DB = 5m + 13n = 14$ , and since the two smallest circles are congruent, $r_{\triangle AED} = r_{\triangle BFD} = m = 2n$ .

Solving $5m + 13n = 14$ and $m = 2n$ gives $m = \cfrac{28}{23}$ and $n = \cfrac{14}{23}$ .

That means $DF = 12n = \cfrac{168}{23}$ , $FC = BC - BF = 13 - 5n = \cfrac{229}{23}$ , $CD = \sqrt{DF^2 + FC^2} = \sqrt{(\frac{168}{23})^2 + (\frac{229}{23})^2} = \cfrac{\sqrt{80554}}{23}$ , and the radius of the largest circle is $r = \frac{1}{2}(DF + FC - CD) = \cfrac{397 + \sqrt{80665}}{46}$ , so that $a = 397$ , $b = 80665$ , $c = 46$ , and $a + b + c = \boxed{81108}$ .

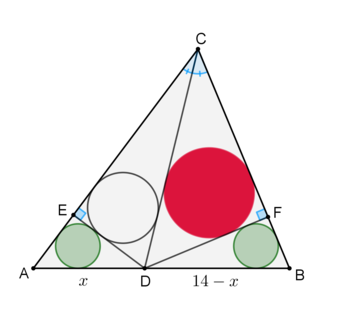$\triangle ABC$ is a compound of a $15$ - $9$ - $12$ and a $13$ - $5$ - $12$ right triangle sharing a common side of length $12$ , which is the height from C of $\triangle ABC$ .
Thus, $\sin A=\dfrac{12}{15}=\dfrac{4}{5} \ \ \ \ \$ , $\ \ \ \ \ \cos A=\dfrac{9}{15}=\dfrac{3}{5} \ \ \ \ \$ , $\ \ \ \ \ \sin B=\dfrac{12}{13} \ \ \ \ \$ and $\ \ \ \ \ \cos B=\dfrac{5}{13}$ .

Let $AD=x$ . Then, $DB=14-x$ .

Moreover, $ED=AD\cdot \sin A\Rightarrow ED=\dfrac{4x}{5}, \ \ \ \ \$ $EA=AD\cdot \cos A\Rightarrow EA=\dfrac{3x}{5}$

For the incircle of the right $\triangle EAD$ we have

$r=\dfrac{1}{2}\left( EA+ED-AD \right)=\dfrac{1}{2}\left( \dfrac{3x}{5}+\dfrac{4x}{5}-x \right)=\dfrac{x}{5} \ \ \ \ \ (1)$ Working similarly on right $\triangle FDB$ , $FD=BD\cdot \sin B\Rightarrow FD=\left( 14-x \right)\dfrac{12}{13}$ $FB=BD\cdot \cos B\Rightarrow FB=\left( 14-x \right)\dfrac{5}{13}$

$r=\dfrac{1}{2}\left( FD+FB-BD \right)=\dfrac{1}{2}\left( 14-x \right)\left( \dfrac{12}{13}+\dfrac{5}{13}-1 \right)=\dfrac{2}{13}\left( 14-x \right) \ \ \ \ \ (2)$ Combining $(1)$ and $(2)$ we get $\dfrac{x}{5}=\dfrac{2}{13}\left( 14-x \right)\Leftrightarrow x=\dfrac{140}{23}$ Using this value, we find $FD=\dfrac{168}{23}$ and $FB=\dfrac{70}{23}$ Hence, by Pythagorean theorem on right $\triangle CDF$ ,

$CD=\sqrt{F{{D}^{2}}+C{{F}^{2}}}=\sqrt{{{\left( \dfrac{168}{23} \right)}^{2}}+{{\left( 13-\dfrac{70}{23} \right)}^{2}}}\Rightarrow CD=\dfrac{\sqrt{80665}}{23}$

Finally, for the inradius $R$ of right $\triangle CDF$ ,

$R=\dfrac{1}{2}\left( FD+CF-CD \right)=\dfrac{1}{2}\left( \dfrac{168}{23}+\dfrac{229}{23}-\dfrac{\sqrt{80665}}{23} \right)\Rightarrow R=\dfrac{397-\sqrt{80665}}{46}$ Doing analogous calculations for the inradius ${R}'$ of $\triangle CDE$ we find ${R}'=\dfrac{373-\sqrt{80665}}{46}$ Since ${R}'<R$ , the largest circle is the incircle of $\triangle CDF$ .

For the answer, $a=397$ , $b=80665$ , $c=46$ , thus, $a+b+c=\boxed{81108}$ .

We note that a $\text{13-14-15}$ triangle is made up of a $\text{3-4-5}$ right triangle and a $\text{5-12-13}$ right triangle sharing an altitude of $12$ . Therefore $\triangle ADE$ is a $\text{3-4-5}$ right triangle and $\triangle BDF$ is a $\text{5-12-13}$ right triangle.

Let $DB=x$ ; then $FB = \frac 5{13}x$ and $DF = \frac {12}{13}x$ . If $r$ is the radius of the two congruent incircles, then

$r = \frac {\frac 12 FB \cdot DF}{\frac 12(FB+DF+DB)} = \frac {2x}{13}$

Similarly, $AD=14-x$ , $AE=\frac 35(14-x)$ . $ED = \frac 45(14-x)$ , and

$r = \frac {\frac 12 AE \cdot ED}{\frac 12(AE+ED+AD)} = \frac {14-x}5$

Therefore $r = \dfrac {2x}{13} = \dfrac {14-x}5 \implies x = \dfrac {182}{23} = DB$ , $DF = \dfrac {12}{13}DB = \dfrac {168}{23}$ , $FB = \dfrac 5{13} DB = \dfrac {70}{23}$ , and $CF = 13-FB = dfrac {229}{23}$ . The radius of the largest circle,

$R = \frac {\frac 12 DF \cdot CF}{\frac 12(DF+CF+CD)} = \frac {DF \cdot CF}{DF+CF+\sqrt{DF^2+CF^2}} = \frac {397-\sqrt{80665}}{46}$

The required answer is $a+b+c = 397+80665+46 = \boxed{81108}$ .