4 Easy Circles
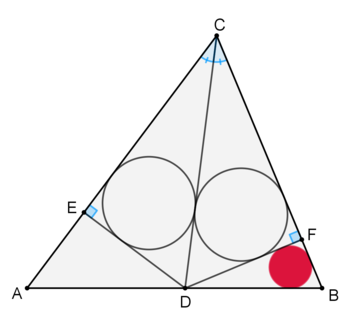
If the two large circles are congruent, what is the radius of the smallest circle?
The answer is 1.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
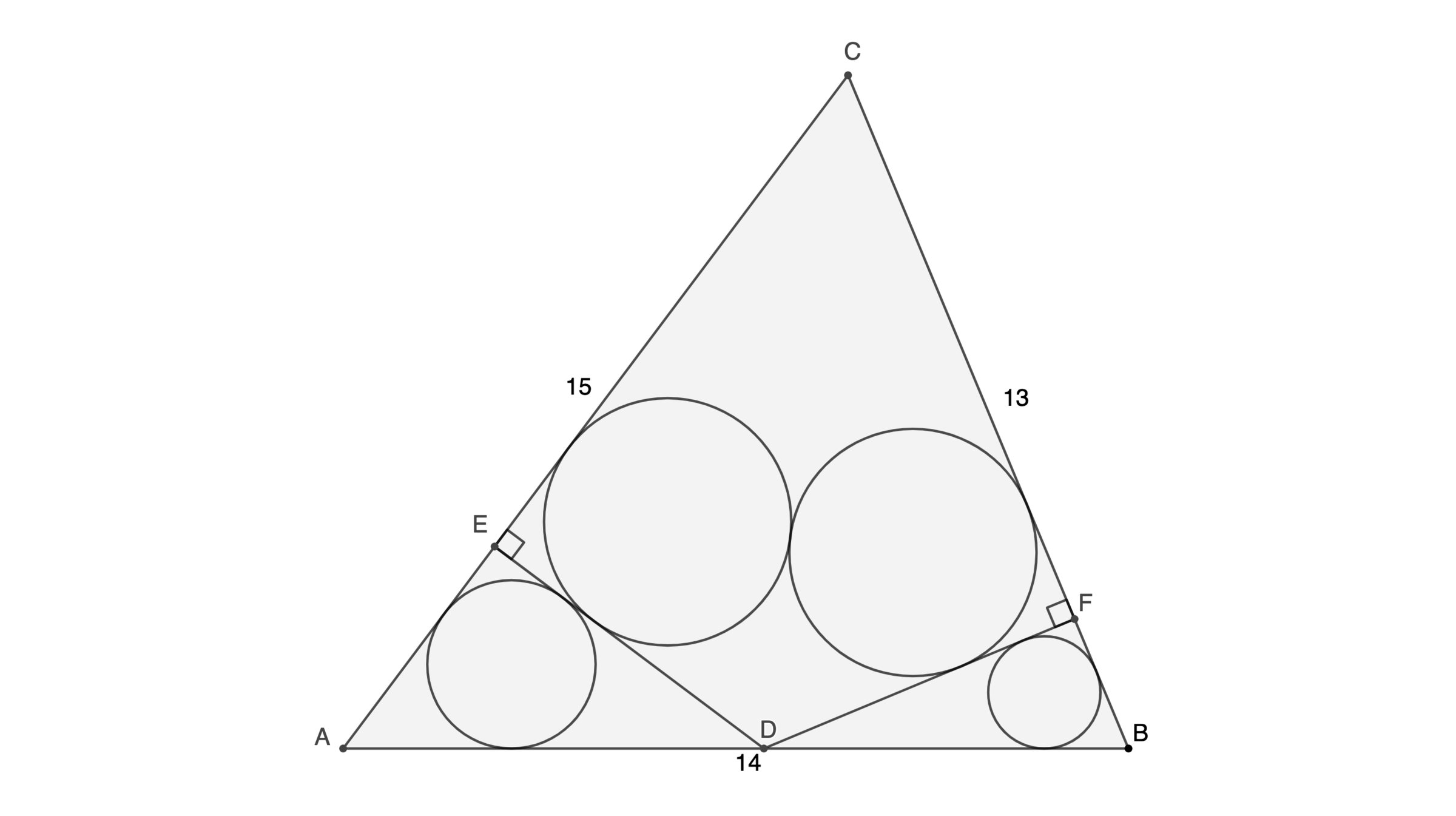
D A D B = b a ⇒ D A + D B D B = a + b a ⇒ A B D B = a + b a ⇒ D B = a + b a c ⇒ D B = 1 3 + 1 5 1 3 × 1 4 ⇒ D B = 6 . 5 The height from C of the 1 3 - 1 4 - 1 5 △ A B C is h c = 1 2 .
Using two different expressions for the area of △ B C D we have
2 1 B C ⋅ D F = 2 1 D B ⋅ h c ⇒ 1 3 × D F = 6 . 5 × 1 2 ⇒ D F = 6 By Pythagorean theorem on right △ F D B ,
F B = D B 2 − D B 2 = 6 . 5 2 − 6 2 ⇒ F B = 2 . 5 Finally, for the radius r of the incircle of △ F D B ,
r = 2 1 ( D F + F B + B D ) [ F D B ] = 2 1 ( D F + F B + B D ) 2 1 D F ⋅ F B = 2 1 ( 6 + 2 . 5 + 6 . 5 ) 2 1 6 × 2 . 5 = 1 Working similarly we find that the incircle of △ E A D equals 1 . 5 , thus the smaller circle is the incircle of △ F D B , hence, the answer is 1 .
The congruency of the two largest circles gives ED = DF. The two smaller right triangles would still be similar to 9-12-15 (left RT) and 5-12-13 (right RT). Considering that both their longer legs are still the same now, and that their hypothenuses have to share the base of length 14 between them, we got the scale of 1/2 (from 14/(13+15) = 1/2) so now what we're looking for is just the incircle of 2.5-6-6.5. Sketching 2+3+10 for the original, the answer is just 2 (original's incircle) times 1/2 (the scale) = 1.
Draw altitude C G . Since the 1 3 - 1 4 - 1 5 triangle is a 9 - 1 2 - 1 5 right triangle combined with a 5 - 1 2 - 1 3 right triangle at side 1 2 , C G = 1 2 .
Now △ A G C ∼ △ A E D and △ B G C ∼ △ B F D by AA similarity, so let A E = 3 m , E D = 4 m , and A D = 5 m (because it is similar to a 9 - 1 2 - 1 5 or 3 - 4 - 5 triangle) and let B F = 5 n , D F = 1 2 n , and D B = 1 3 n (because it is similar to a 5 - 1 2 - 1 3 triangle).
From segment addition, A B = A D + D B = 5 m + 1 3 n = 1 4 , and by symmetry of the two large circles, E D = D F = 4 m = 1 2 n .
Solving 5 m + 1 3 n = 1 4 and 4 m = 1 2 n gives m = 2 3 and n = 2 1 .
Therefore, the radius of the smallest circle is r = P △ B F D 2 A △ B F D = B F + D F + D B 2 ⋅ 2 1 ⋅ B F ⋅ D F = 5 n + 1 2 n + 1 3 n 5 n ⋅ 1 2 n = 3 0 n 6 0 n 2 = 2 n = 2 ⋅ 2 1 = 1 .
We note that △ C D E and △ C D F are congruent. This means that C D bisects ∠ C and by angle bisector theorem ,
A B D B = C A B C ⟹ 1 4 − D B D B = 1 5 1 3 ⟹ D B = 1 5 + 1 3 1 3 ⋅ 1 4 = 6 . 5
We also note that a 13-14-15 triangle is made up of a 3-4-5 right triangle and a 5-12-13 right triangle sharing an altitude of 1 2 ; and that △ B D F is a 5-12-13 right triangle. Since D B = 6 . 5 , B F = 1 3 5 ⋅ 6 . 5 = 2 . 5 and D F = 1 3 1 2 ⋅ 6 . 5 = 6 . And the radius of the incircle of △ B D F ,
r = 2 1 ( B F + D F + D B ) 2 1 B F ⋅ D F = 2 . 5 + 6 + 6 . 5 2 . 5 ⋅ 6 = 1