4 Hats, 1 Executioner

Logic Level 1

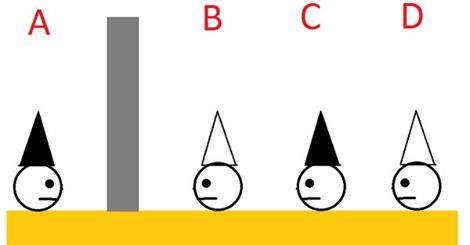
Shown above are four men buried up to their necks in the ground. They cannot move, so they can only look forward. Between A and B is a brick wall which cannot be seen through. They all know that between them they are wearing four hats--two black and two white--but they do not know what color they are wearing. Each of them know where the other three men are buried.

In order to avoid being shot, one of them must call out to the executioner the color of their hat. If they get it wrong, everyone will be shot. They are not allowed to talk to each other and have 10 minutes to fathom it out.

After one minute, one of them calls out.

Question: Which one of them calls out?

Why is he 100% certain of the color of his hat?

Note: This is not a trick question. There are no outside influences nor other ways of communicating. They cannot move and are buried in a straight line; A & B can only see their respective sides of the wall, C can see B, and D can see B & C.

B D A C

4 solutions

Brian Charlesworth
Jul 24, 2015

If D saw either two black or two white hats ahead of him then he would know that he would have a white or black hat, respectively. Since he in fact sees one of each color ahead of him means that he can't make any immediate conclusions on the color of his own hat. The fact that D does not then immediately say something makes it apparent to the others that D sees one hat of each color, and since C sees a white hat in front of him allows him to conclude that he himself has a black hat.

I like this problem, but I really have to disagree with the answer. The answer is conditional.

If D sees two of the same colors in front of him, then $\boxed{D}$ will shout his hat color with 100% certainty.

If D sees two different colors in front of him, then D waits, and then $\boxed{C}$ shouts his hat color with "100% certainty"; but C is assuming that D plays optimally. What if D is dumb, or D doesn't perform well under pressure? How long does it take D to think?

I guess I'm just looking into it too much, though. My point is that it lacks a scenario where you have 100% certainty. There's no prior communication indicating how long another person will wait if they can't be certain about their hat color.

Brock Brown - 5 years, 10 months ago

You have a point, (they're all wearing dunce caps, after all), but it is "normal" to assume in this type of question that, unless stated otherwise, all those involved are highly (and equally) competent and logical. As such, a minute of silence is more than enough time to allow C to be certain of his hat color. The question is already long enough, but perhaps it could be stated at the beginning that there are "four highly competent and logical men" involved, to avoid any uncertainty. And by "competent" I mean that they are able to perform under pressure. :)

Brian Charlesworth - 5 years, 10 months ago

Yeah, I would agree with Brock and Brian that it should be stated somehow that they all are "highly competent" or something similar. We cannot somehow infer from anything given that D cannot decide.

Domas Vaitmonas - 5 months ago

Hoang Truong
Jul 27, 2015

D see B and C,because B and C wear black and white hats respectively so D cannot ensure what color of the hat he is wearing......C see B,because B wear a white hat so if C also wear a white hat D will call out, but D didn't call out so C knew that he was wearing a black hat p/s:sorry for my bad english

Tina Haiser
Feb 2, 2020

It's C. Because he knows that D can see two people and if they both had the same color hat D would know the color of his hat and would call it out. After a minute C knows that D is seeing two different colors and C is seeing a white hat so his hat must be black.

Tri Nugroho
Jul 26, 2015

There are two black hats and 2 white hats. Hat there are six possible combinations are: WWBB, WBWB, BWWB, WBBW, BWBW, BBWW 4th people to see in front of three people to wear a white hat and the second to wear black hats, so there is the possibility of people to wear hats 4th black or white hats. He could not answer. Because the 4th can not answer, then it is likely a combination hat and WBBW BWWB be removed from the list. Now stay 4 combination is WWBB, BWBW, WBWB, BBWW. 3th people to know that people can not answer to the fourth and two in front of people to wear black hats, the combination of which may stay WWBB and BWBW. So whatever combination he's wearing a black hat.

4 Hats, 1 Executioner

4 solutions

0 pending reports