4 in 5
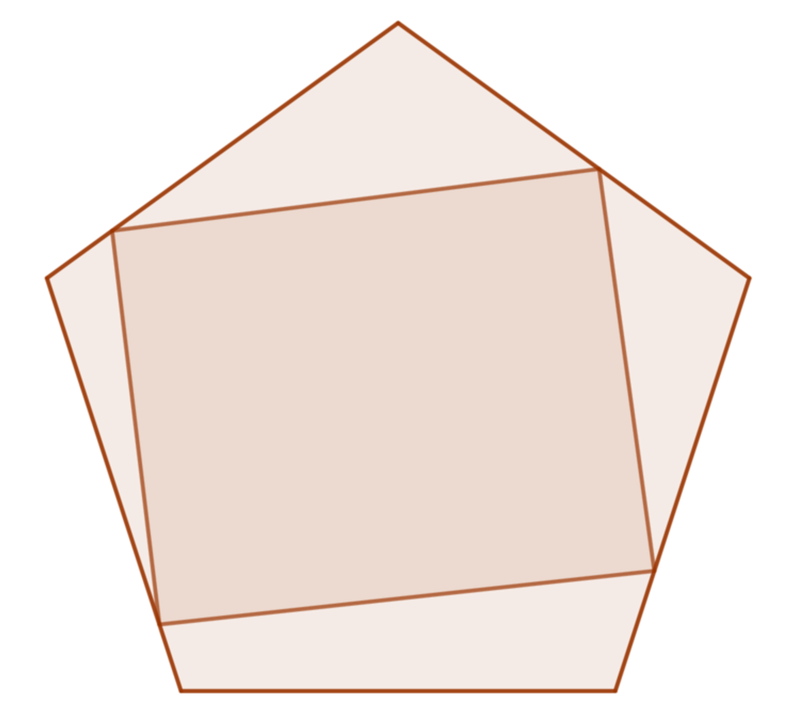
A square is inscribed in a regular pentagon such that all four vertices touch the pentagon. If the side length of the pentagon is 1 and the side length of the square is s , find ⌊ 1 0 0 0 0 s ⌋ .
The answer is 10604.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
One of the reasons I love mathematics is that it's such an unexpected platform for creativity. There are so many original ways to approach a problem. Thank you, Chew-Seong, for demonstrating this once again. By the way, I find a certain beauty in your penultimate expression of the solution, sin 3 8 ∘ + sin 1 8 ∘ sin 1 0 8 ∘ .
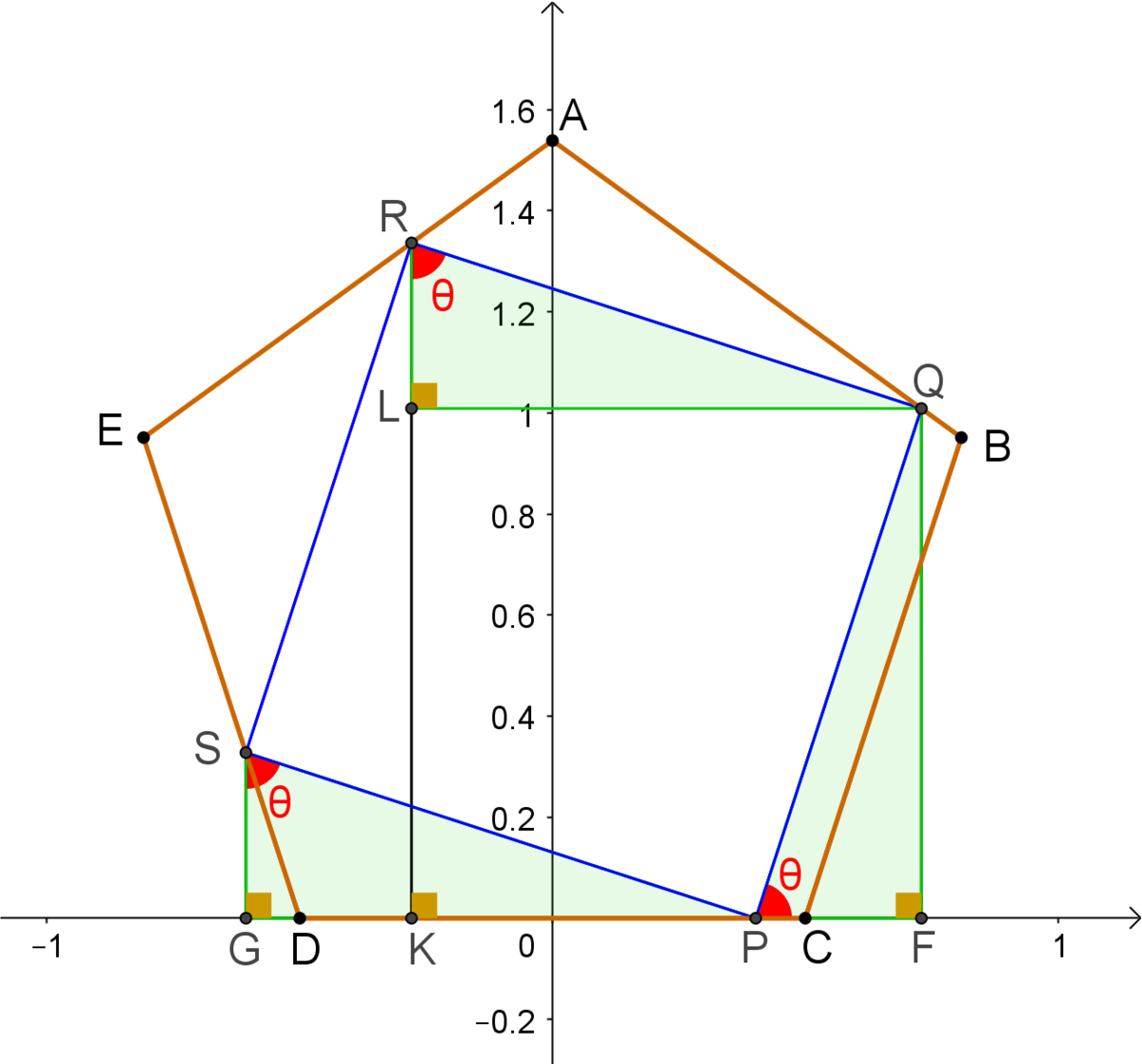 We place the regular pentagon
A
B
C
D
E
on the plane so that
C
D
lie on the x-axis and
a
on the positive part of y-axis. The four vertices
P
,
Q
,
R
,
S
of the square will lay on four of the pentagon’s sides. Let them be
C
D
,
A
B
,
A
E
, and
E
D
respectively. From points
Q
,
R
and
S
we drop perpendicular to the axes, thus forming three congruent right triangles
△
P
Q
F
,
△
R
Q
L
and
△
S
P
G
. Let
∠
Q
P
F
=
∠
Q
R
L
=
∠
P
S
G
=
θ
. Denote by
x
the x-coordinate of
P
/ and by
s
the side length of the square.
Then, we have
We place the regular pentagon
A
B
C
D
E
on the plane so that
C
D
lie on the x-axis and
a
on the positive part of y-axis. The four vertices
P
,
Q
,
R
,
S
of the square will lay on four of the pentagon’s sides. Let them be
C
D
,
A
B
,
A
E
, and
E
D
respectively. From points
Q
,
R
and
S
we drop perpendicular to the axes, thus forming three congruent right triangles
△
P
Q
F
,
△
R
Q
L
and
△
S
P
G
. Let
∠
Q
P
F
=
∠
Q
R
L
=
∠
P
S
G
=
θ
. Denote by
x
the x-coordinate of
P
/ and by
s
the side length of the square.
Then, we have
P ( x , 0 ) Q ( x + s ⋅ cos θ , s ⋅ sin θ ) R ( x + s ⋅ cos θ − s ⋅ sin θ , s ⋅ sin θ + s ⋅ cos θ ) S ( x − s ⋅ sin θ , s ⋅ cos θ ) The y-coordinate of vertex A is the height of the pentagon, thus A ( 0 , 2 5 + 2 5 ) .
The equations of line A B is
y = − ( tan 3 6 ∘ ) x + 2 5 + 2 5 ⇔ y = − 5 − 2 5 x + 2 5 + 2 5
The equations of line A E is
y = ( tan 3 6 ∘ ) x + 2 5 + 2 5 ⇔ y = 5 − 2 5 x + 2 5 + 2 5
The equations of line D E is
y = ( tan 1 0 8 ∘ ) ( x + 2 1 ) x ⇔ y = − 5 + 2 5 ( x + 2 1 )
Since Q ∈ A B , R ∈ A E and S ∈ D E , we get the system ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ s ⋅ sin θ s ⋅ sin θ + s ⋅ cos θ s ⋅ cos θ = − 5 − 2 5 ( x + s ⋅ cos θ ) + 2 5 + 2 5 = 5 − 2 5 ( x − s ⋅ sin θ + s ⋅ cos θ ) + 2 5 + 2 5 = − 5 + 2 5 ( x − s ⋅ sin θ + 2 1 ) Settting y = s ⋅ sin θ and z = s ⋅ cos θ , we come to a linear 3x3 system:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ y y + z z = − 5 − 2 5 ( x + z ) + 2 5 + 2 5 = 5 − 2 5 ( x − y + z ) + 2 5 + 2 5 = − 5 + 2 5 ( x − y + 2 1 ) which solves to
x
≈
0
.
4
0
2
1
1
3
0
3
2
5
9
0
3
0
7
,
y
≈
1
.
0
0
8
5
9
3
0
3
2
1
3
0
2
0
,
z
≈
0
.
3
2
7
7
1
1
7
4
1
6
2
2
3
7
2
Now we have,
s
2
=
s
2
⋅
(
sin
2
θ
+
cos
2
θ
)
=
(
s
⋅
sin
θ
)
2
+
(
s
⋅
cos
θ
)
2
=
y
2
+
z
2
≈
(
1
.
0
0
8
5
9
3
0
3
2
1
3
0
2
0
)
2
+
(
0
.
3
2
7
7
1
1
7
4
1
6
2
2
3
7
2
)
2
=
1
.
1
2
4
6
5
4
8
9
0
0
5
8
7
5
Hence,
s
=
1
.
1
2
4
6
5
4
8
9
0
0
5
8
7
5
≈
1
.
0
6
0
4
9
7
4
7
2
9
1
4
8
4
.
For the answer, ⌊ 1 0 0 0 0 s ⌋ = 1 0 6 0 4 .
I think your insight regarding the three congruent triangles is ingenious. I wish I had noticed that. And a beautiful exposition. Thank you, Thanos.
Log in to reply
Thank you Fletcher. I'm glad you like it.
While I can't prove it, I'm pretty certain the square must be oriented symmetrically to the pentagon, i.e. a side of the square must be parallel to a side of the pentagon, as in the figure. In fact, I suspect this is the only way to inscribe a square. If someone knows, I'd be grateful to learn more.
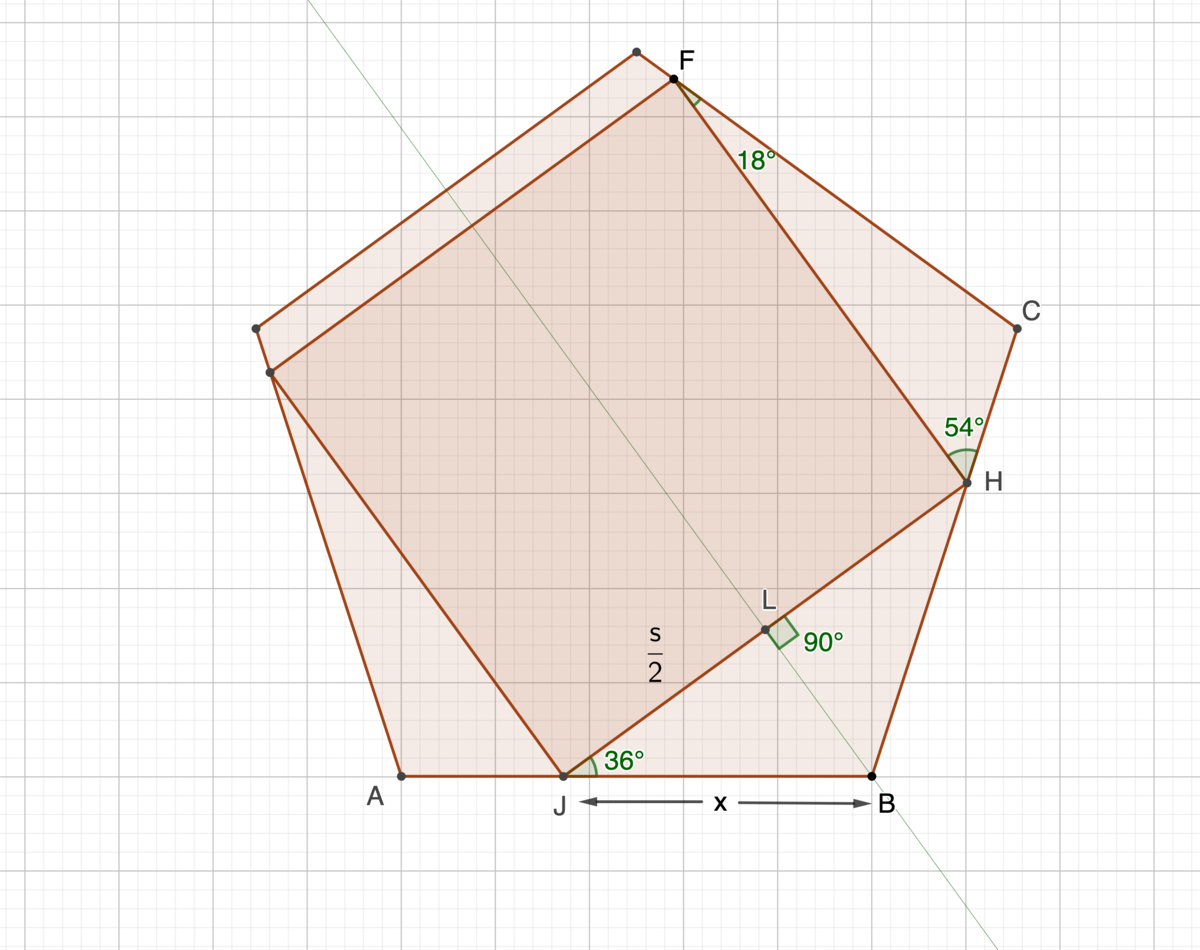
Symmetry implies △ J B H is isosceles, and thus J B = B H . Let L B bisect ∠ A B C .
Since ∠ B = 1 0 8 ∘ , ∠ S H B = 3 6 ∘ , ∠ F H C = ( 1 8 0 ∘ − 9 0 ∘ − 3 6 ∘ ) = 5 4 ∘ .
Similarly ∠ H F C = ( 1 8 0 ∘ − 5 4 ∘ − 1 0 8 ∘ ) = 1 8 ∘ .
Let s = J H and x = J B .
Using the law of sines on △ H F C , sin 1 0 8 ∘ s = sin 1 8 ∘ 1 − x .
From the right △ J L B , s = 2 x ⋅ cos 3 6 ∘
Substituting for s , sin 1 0 8 ∘ 2 x cos 3 6 ∘ = sin 1 8 ∘ 1 − x
Let k = sin 1 0 8 ∘ cos 3 6 ∘ sin 1 8 ∘ ⟹ x = 2 k + 1 1
Evaluating , x = 2 1 ( 5 − 5 − 2 5 − 2 5 ) ≈ 0 . 6 5 5 4 2 3
Evaluating , s = 5 − 2 1 ( 5 − 5 ) ≈ 1 . 0 6 0 4 9 7
So the requested answer is 1 0 6 0 4
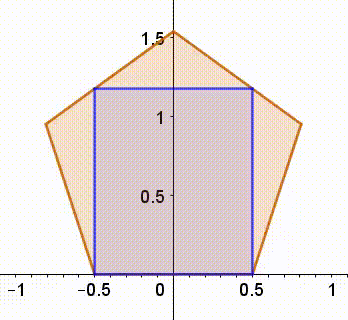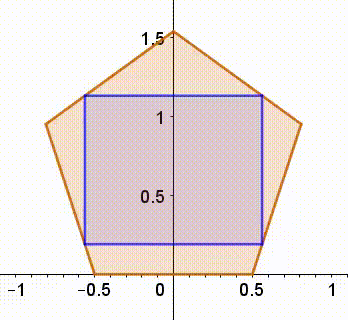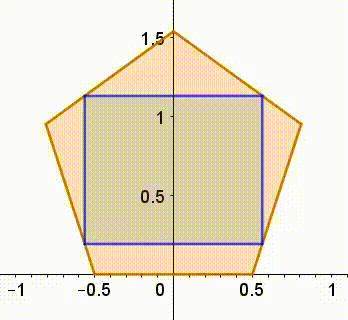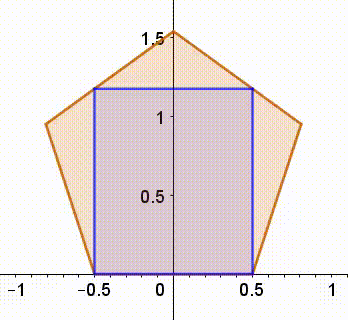 Your intuition about the existence of a square oriented this way is correct. We can easily use a continuity argument as the animation implies. The uniqueness of this solution is not obvious to me. That's why, in the solution I'm about to post, I use a different approach.
Your intuition about the existence of a square oriented this way is correct. We can easily use a continuity argument as the animation implies. The uniqueness of this solution is not obvious to me. That's why, in the solution I'm about to post, I use a different approach.
Consider a general case of a quadrilateral F G H I inscribed in the unit regular pentagon A B C D E . Let F G = I F = s 1 , F G ⊥ I F , F G ⊥ G H , ∠ I F J = θ and G H = s 2 (note that s 2 > s 1 for θ = 5 ∘ as shown in the figure). Then the various angles in terms of θ are as shown. If D F = a , then E F = 1 − a and F J = 1 + 2 a sin 1 8 ∘ . By sine rule , we have:
sin ( 5 4 ∘ + θ ) 1 − a = sin 1 0 8 ∘ s 1 = sin ( 7 2 ∘ − θ ) 1 + 2 a sin 1 8 ∘ ⟹ s 1 = sin ( 7 2 ∘ − θ ) + 2 sin 1 8 ∘ sin ( 5 4 ∘ + θ ) sin 1 0 8 ∘ ( 2 sin 1 8 ∘ + 1 )
Let E G = b . By sine rule, b = sin 1 0 8 ∘ s 1 sin ( 1 8 ∘ − θ ) and
sin 1 0 8 ∘ s 2 s 2 = sin ( 3 6 ∘ + θ ) 1 − b = sin ( 3 6 ∘ + θ ) sin 1 0 8 ∘ − s 1 sin ( 1 8 ∘ − θ )
When quadrilateral F G H I is a square s 2 = s 1 = s , then
⟹ s 1 sin ( 7 2 ∘ − θ ) + 2 sin 1 8 ∘ sin ( 5 4 ∘ + θ ) sin 1 0 8 ∘ ( 2 sin 1 8 ∘ + 1 ) ( 2 sin 1 8 ∘ + 1 ) ( sin ( 3 6 ∘ + θ ) + sin ( 1 8 ∘ − θ ) ) = sin ( 3 6 ∘ + θ ) + sin ( 1 8 ∘ − θ ) sin 1 0 8 ∘ = sin ( 3 6 ∘ + θ ) + sin ( 1 8 ∘ − θ ) sin 1 0 8 ∘ = sin ( 7 2 ∘ − θ ) + 2 sin 1 8 ∘ sin ( 5 4 ∘ + θ )
Solving the equation above, we get θ = 0 ∘ . And s = sin 3 6 ∘ + sin 1 8 ∘ sin 1 0 8 ∘ ≈ 1 . 0 6 0 4 9 7 4 7 3 ⟹ ⌊ 1 0 0 0 0 s ⌋ = 1 0 6 0 4 .