4-Panned Balance
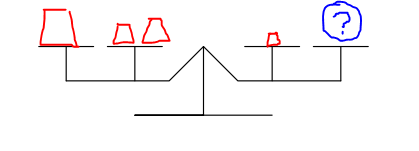You have a balance with fulcrum at
and pans at
,
(as shown in the diagram). Find the least number of positive integer weights you need in order to measure any integer weight from 1 to 1000.
Note that any number of weights can be placed in any of the 4 pans (even the pan with the object you want to weigh).
Clarification: You want to be able to weigh the integer weights from 1 to 1000, but you should not assume that the object you weigh will have an integer weight.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I believe that putting weight in distant-from-fulcrum pan is balanced by putting twice the weight in opposing near-the-fulcrum pan. I know it's well-known in physics, but I believe it should be mentioned in the problem.
Not a complete solution here, I can't solve it yet but probably my work can help a bit. For every n different standard weight, we can put each in pan a, pan b, pan c, pan d, or not put the weight. This will cause 5^n possibility. Note that not putting anything at all doesn't contribute to weighing, so there are 5^n - 1 cases remaining. Note that each possibility has complete opposite, and that the case of having standard weighs in opposing position are actually similar. now we can observe (5^n - 1)/2 different cases. We're still assuming the perfect condition that each cases can get balanced by two different non-standard weight (because the non-standard weight can be put in distant pan or near pan. Now with n standard weight in this perfect condition, we can weigh 5^n - 1 non-standard weight.
However, we also can tell that to measure certain integer weight we don't have to get the perfect balance. For example, we can measure a non-standard 1 kg weight just by knowing that it's lighter than a 2 kg standard weight. Now if we assume the perfect condition such that all of those 5^n - 1 different condition can be used to balance 5^n - 1 different even weights, we can assume that we actually can measure 2 (5^n -1) different integer weights. In this case, n= 4 should be enough to measure 1000 first integer weights. I have a hard time deciding the case where it can work, but if it doesn't work, then obviously the problem is extreme double-counting.
For n=5, we can use 2, 10, 50, 250, and 1250 to measure up to 3124 different weights