4 semis in a square
Four congruent semicircles are packed into a square.
What proportion of the square is filled?
The answer is 0.8417872145.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I looked at it as putting one circle in the middle with one fourth of a circle with the same radius at each corner. This means that the radius would be one fourth of root 2 if the side of the square would be 1 unit. If you square the radius of one circle you get one eight. One eight times pi times 2 (two circles total) you get 0.785 for the area covered by two congruent circles covering one square with a side = 1 unit.
Log in to reply
I did the same and got the same answer (2π/8), but then I saw that the circles were touching the corners of the square, that was the key of the problem I guess.
Wait... How do we prove/know that the line connecting the centres of two adjacent semicircles will pass through the point of intersection of the semicircles?
Log in to reply
The radii from the centers of two circles (not necessary the same radius) is perpendicular to the tangent at the point the two circles touch. The angle between the two radii is 180 ∘ , which means the two radii form a straight line.
Exactly what I did, great job!
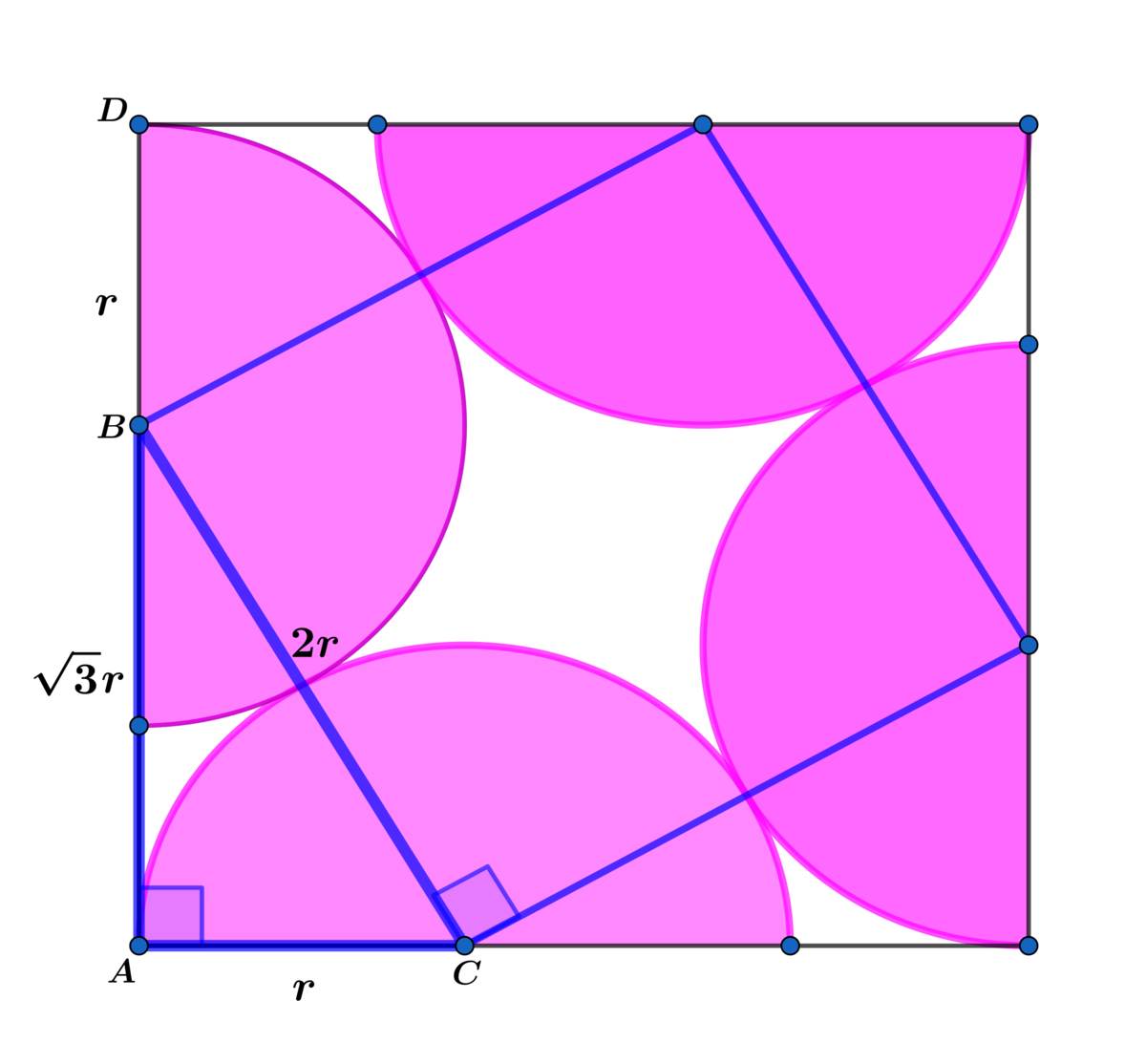
In right △ A B C , B C = 2 r and A C = r ⟹ A B = 3 ⟹ B D = r
⟹ A s q u a r e = ( 3 + 1 ) 2 r 2 and A c i r c l e s = 2 π r 2 ⟹ A s q u a r e A c i r c l e s = ( 3 + 1 ) 2 2 π ≈ 0 . 8 4 1 7 8 7 2 1
If circle radius is taken as unity, we can show by construction ( joining centers of two tangent adjoining circles) that side of square=2/{(√3)-1}.
This gives the area ratio of four semi circles to square as (π/2)[{(√3)-1}^2]=0.8417.
Answer=0.8417
You probably meant circle diameter is taken as unity.

The centers of two tangent semicircles and their point of tangency are collinear because the two radii that join the centers to the point of tangency are both perpendicular to the same tangent at the same point. Therefore, the image to the left is a right triangle. If the radius of the circle is r , the length of the longer leg is ( 3 ) r .
The length of the entire square's side is ( 3 ) r + r = ( 3 + 1 ) r . The desired proportion is ( ( 3 + 1 ) r ) 2 4 ( 2 1 π r 2 ) ≈ 0 . 8 4 1 8 .
Let the square be a unit square with side length and area of 1 and the radius of the semicircles be r , We note that the centers of two adjacent semicircles and the square vertex between them form a right triangle with side lengths of 1 : 3 : 2 .
Therefore, we have r + 3 r = 1 , ⟹ r = 1 + 3 1 and the ratio of the area of the 4 semicircles to the area of the square is: A □ 2 A ◯ = ( 1 + 3 ) 2 2 π ≈ 0 . 8 4 2 , since A □ = 1 .