4- The Sequence

Number Theory Level 2

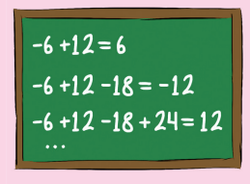The sequence -6, 12, -18, 24, -30, 36, ... is obtained from the positive multiples of 6, the terms multiplying by -1 in the odd positions. Note in the figure that the sum of the first two terms of the sequence is equal to 6 and the sum of the first three terms is equal to -12. How many consecutive terms of this sequence we must add, from the first, to get 180 as a result?


The answer is 60.

Victor Paes Plinio by Victor Paes Plinio , 21, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

We must look at the results of the sums. They form the following sequence: -6,6,-12,12,-18,18,-24,24,..... So we can say that we have 2 arithmetic progressions: 6,12,18,24,.... and -6,-12,-18,-24,... Taking one of them and appliyng the general term formula of an AP, we have: a n = a 1 + ( n − 1 ) . r a_{n} = a_{1} + (n - 1).r ; 180 = 6 + ( n − 1 ) . 6 180 = 6 + (n - 1).6 ; n = 30 n = 30 ; But we have to double this result, since we also have the negative numbers. So, the answer is 60.

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Jack Rawlin
Dec 24, 2014

The addition of two consecutive terms - where the first term is negative - will always equal six

So since 180 6 = 30 \frac {180}{6} = 30 we can say that thirty lots of negative-positive term sets equals one hundred and eighty. Since each term set contains two terms we can just multiply thirty by two to get sixty terms.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...