4 tiles
You have the following and and tiles:
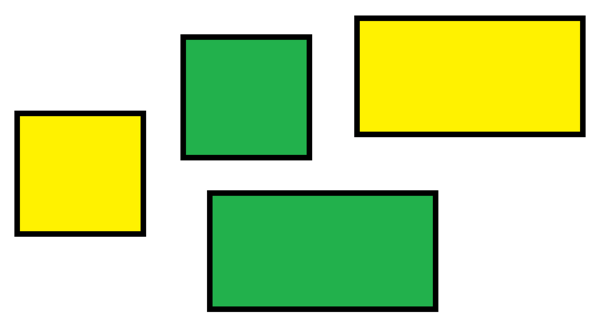
How many ways can you use them to tile a grid?
Assumptions :
- The entire grid must be covered
- No overlaps or tiles outside the boundary
- The tiles can be oriented veritcally or horizontally
- You have exactly what is pictured, i.e. 1 green tile of each size and 1 yellow tile of each size
The answer is 44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Forget the colors for now...
For the 1x2 tiles they can be oriented:
Total: 11 ways
Now add in the colors:
For each of the above combinations, the colors on the squares can be exchanged (x2) and the colors on the rectangles can be exchanged (x2).
Total = 1 1 ⋅ 2 ⋅ 2 = 4 4 ways