4 5 ° is everywhere
M and N are points on hypotenuse A B of right triangle A B C such that A M = 3 , N B = 4 .
If all three of the yellow angles measure the same, what is the area of △ A B C ?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Since ∠ A C B = 9 0 ∘ then ∠ A = ∠ B = 4 5 ∘ = ∠ M C N . Let A C = a . Since ∠ A = ∠ B then A C = B C = a . Let ∠ A C M = θ , then ∠ C M A = 1 8 0 ∘ − 4 5 ∘ − θ = 1 3 5 ∘ − θ . By sine rule : A M A C = 3 a = sin ∠ A C M sin ∠ C M A = sin θ sin ( 1 3 5 ∘ − θ )
And ∠ N C B = 9 0 ∘ − 4 5 ∘ − θ = 4 5 ∘ − θ and ∠ C N B = 1 8 0 ∘ − 4 5 ∘ − ( 4 5 ∘ − θ ) = 9 0 ∘ + θ . By sine rule again: N B B C = 4 a = sin ( 4 5 ∘ − θ ) sin ( 9 0 ∘ + θ ) .
Then we have:
a = sin θ 3 sin ( 1 3 5 ∘ − θ ) sin θ 3 ( 2 1 cos θ + 2 1 sin θ ) 2 3 ( cos 2 θ − sin 2 θ ) 2 3 cos 2 θ ⟹ tan 2 θ 1 − tan 2 θ 2 tan θ 3 tan 2 θ + 8 tan θ − 3 ( 3 tan θ − 1 ) ( tan θ + 3 ) ⟹ tan θ = sin ( 4 5 ∘ − θ ) 4 sin ( 9 0 ∘ + θ ) = 2 1 cos θ − 2 1 sin θ 4 cos θ = 4 sin θ cos θ = 2 sin 2 θ = 4 3 = 4 3 = 0 = 0 = 3 1 As θ < 9 0 ∘
Now we have:
a = sin ( 4 5 ∘ − θ ) 4 sin ( 9 0 ∘ + θ ) = 2 1 cos θ − 2 1 sin θ 4 cos θ = 1 − tan θ 4 2 = 1 − 3 1 4 2 = 6 2
Therefore, the area of △ A B C : A = 2 a 2 = 3 6 .
We reflect A to M C line. If we get the Q point, then
Q C = A C , ∠ Q C M = ∠ A C M .
We reflect B to N C line. If we get the R point, then
R C = B C , ∠ R C N = ∠ B C N .
If ∠ A C M = α , then ∠ Q C M = α , and if ∠ B C N = β , then ∠ R C N = β .
If
Q
and
R
is not the same point, then
∠
M
C
N
=
α
+
β
+
∠
Q
C
R
or
∠
M
C
N
=
α
+
β
−
∠
Q
C
R
. (It depends on that
Q
is near to
B
and
R
is near to
A
, or inversely.) We know that
∠
M
C
N
=
4
5
°
, so
∠
A
C
B
=
9
0
°
−
∠
Q
C
R
or
∠
A
C
B
=
9
0
°
+
∠
Q
C
R
. But
∠
A
C
B
=
9
0
°
, so it is impossible unless
Q
and
R
is the same point. (Let
P
the point which was
R
and
Q
.)
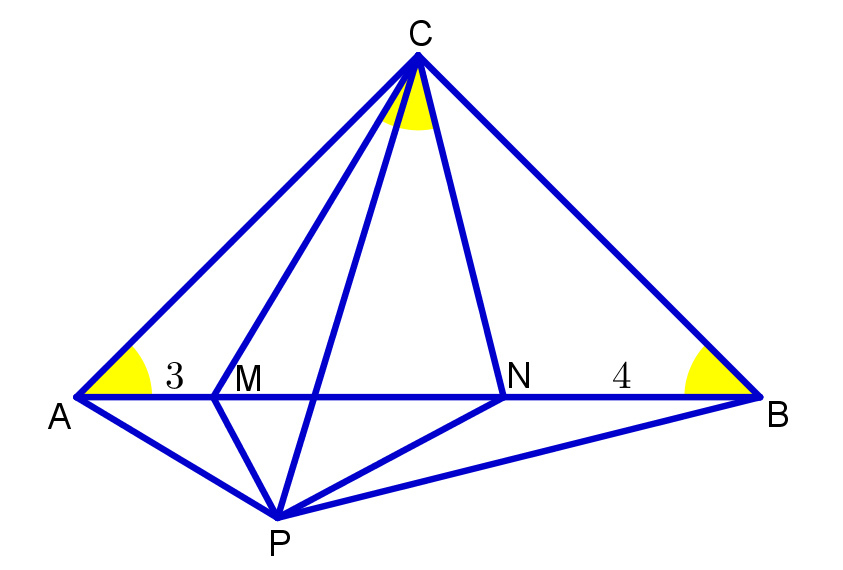 By the reflection we get:
By the reflection we get:
∠ M P C = ∠ M A C = 4 5 °
∠ N P C = ∠ N B C = 4 5 °
∠ M P N = ∠ M P C + ∠ N P C = ∠ M A C + ∠ N B C = 9 0 °
So the N M P triangle is right-angled. Using Pythagoras-theorem: M N 2 = P M 2 + P N 2 .
Since P M = A M and P N = N B , M N 2 = A M 2 + N B 2 . So M N = M N 2 = 3 2 + 4 2 = 5 .
From that A B = 3 + 4 + 5 = 1 2 and
[ A B C ] = 2 A B ∗ 2 A B = 3 6
No trigonometry, a beautiful solution
Note that ∠ A C N = ∠ A C M + ∠ M C N = ∠ A C M + ∠ C A M = ∠ C M B and ∠ A = ∠ B so △ A C N ∼ △ B M C . Since △ A C B is 4 5 ∘ − 4 5 ∘ − 9 0 ∘ , we have B C = A C , A B = A C 2 and M N = A B − A M − N B = A C 2 − 7 , from which it follows that A N = A M + M N = A C 2 − 4 and M B = M N + N B = A C 2 − 3 . From the stated similarity, B M A C = B C A N . Substituting into this last proportion yields A C 2 − 3 A C = A C A C 2 − 4 . Now solve for A C to obtain A C = 2 , an impossibility, or A C = 6 2 . This last value implies the requested area is 2 A C 2 = 3 6 .
Let A M = p , M N = r , and N B = q . We will first show the interesting fact that p 2 + q 2 = r 2 .
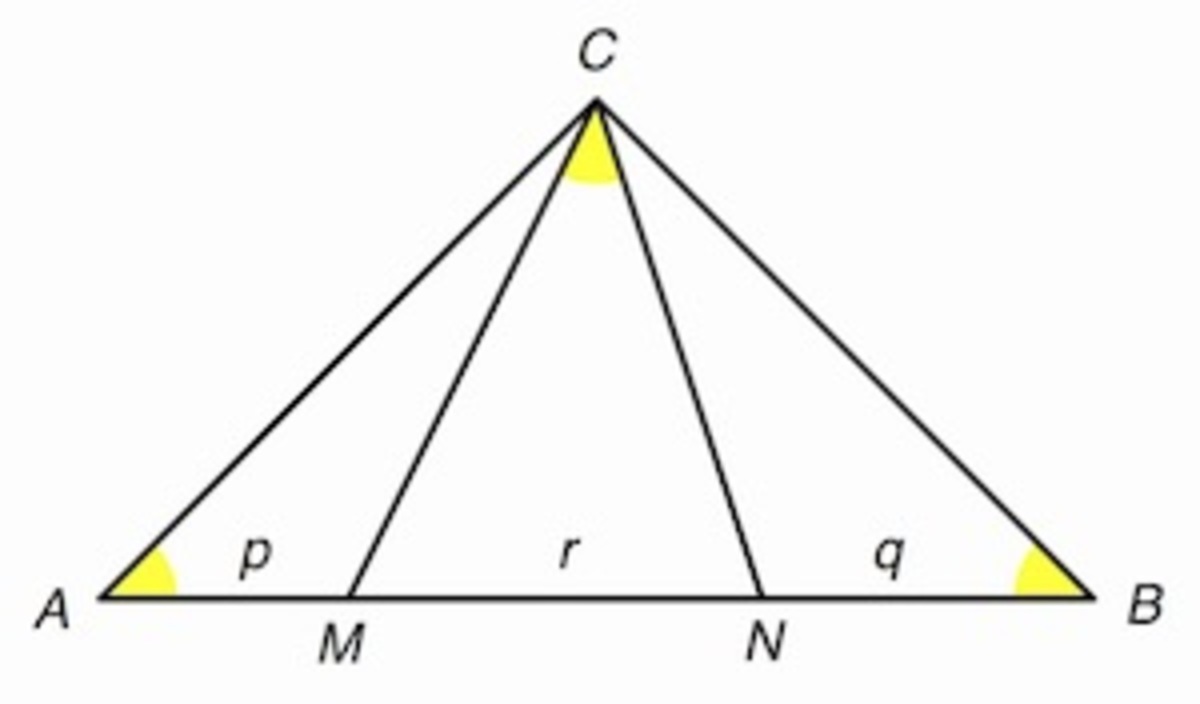
Draw N P so that N P = N B and ∠ C N P = ∠ C N B . Draw C P .
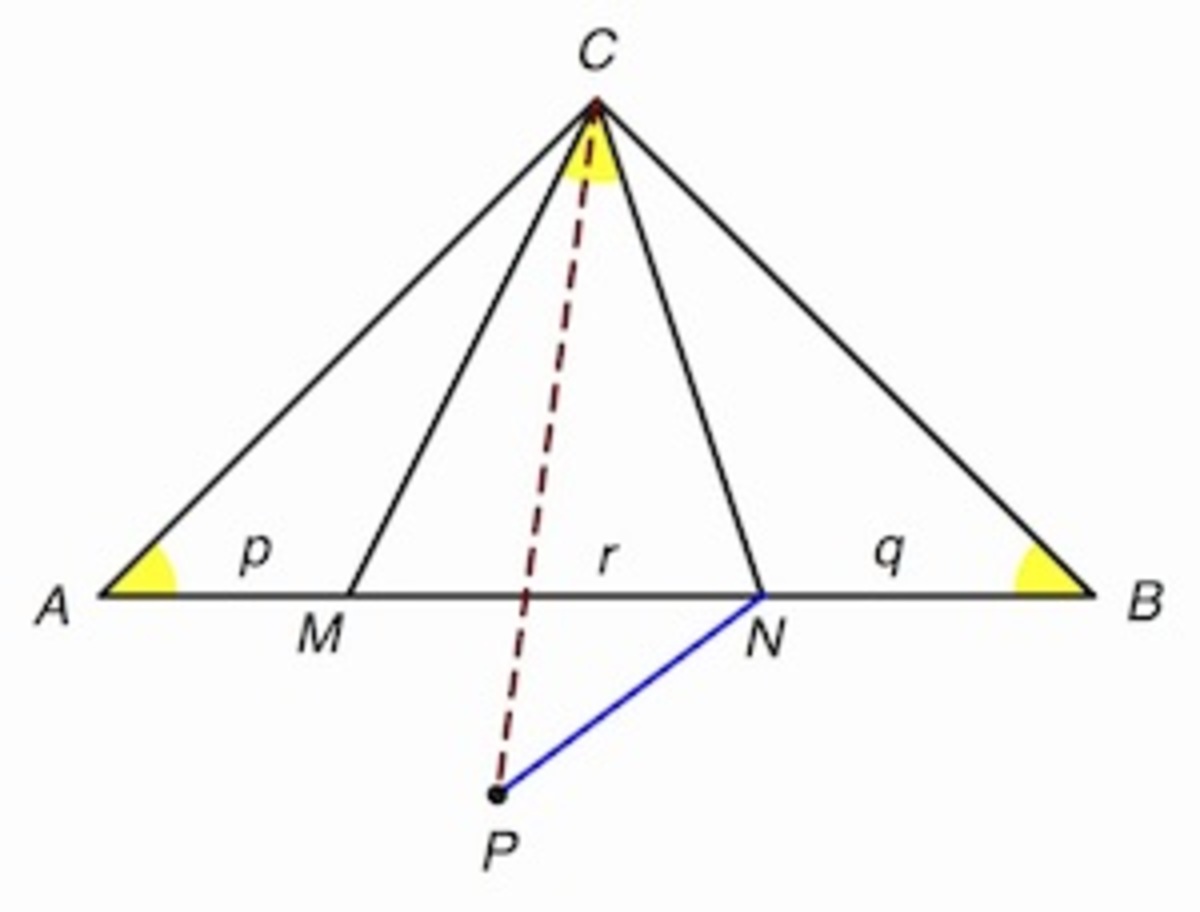
△ C N B ≅ △ C N P by SAS, so C P = C B and ∠ P C N = ∠ B C N . Now draw P M .
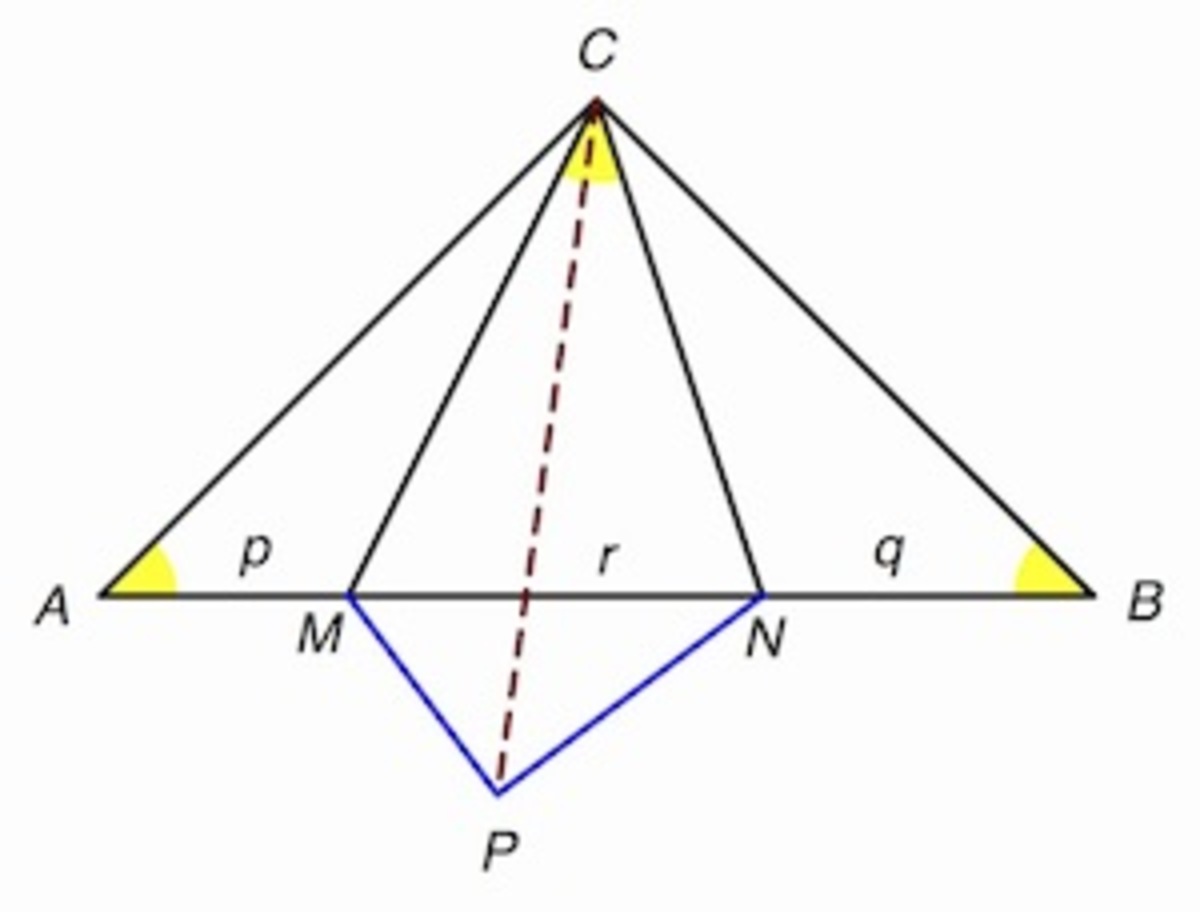
Now ∠ A C M = ∠ A C B − ∠ M C N − ∠ N C B = 9 0 ∘ − 4 5 ∘ − ∠ N C B = 4 5 ∘ − ∠ N C B = ∠ M C N − ∠ P C N = ∠ P C M .
So ∠ A C M = ∠ P C M and C P = C B = C A , so △ A C M ≅ △ P C M by SAS. Thus, P M = A M = p .
Triangle M P N is a right triangle because ∠ C P M = ∠ C A M = 4 5 ∘ and ∠ C P N = ∠ C B N = 4 5 ∘ .
So P M = p , N P = q , and M N = r , and by the Pythagorean Theorem, p 2 + q 2 = r 2 .
Now, getting back to the original problem, p = 3 and q = 4 , so r = 5 . Therefore, A B = 1 2 which implies that the area of △ A B C = 3 6 .
Let M N = x , A C = B C = y
Pythagorean theorem on Δ A B C
( x + 7 ) 2 = y 2 + y 2 ⇔ x 2 + 1 4 x + 4 9 = 2 y 2 (1)
.
Δ A N C ≈ Δ B C M
B M A C = B C A N ⇔ x + 4 y = y x + 3 ⇔ y 2 = x 2 + 7 x + 1 2 (2)
.
From (1) and (2) x = 5 and y 2 = 7 2
The area of Δ A B C is : [ A B C ] = 2 y 2 = 2 7 2 = 3 6
Let
O
be the midpoint of side
A
B
ˉ
, then it is obvious it's the perpendicular
bisector, hence,
A
O
ˉ
=
B
O
ˉ
=
C
O
ˉ
= x, then since
∠
M
C
N
is 45,
t
a
n
−
1
(
x
x
−
3
) +
t
a
n
−
1
(
x
x
−
4
) =
4
π
then using t a n ( a + b ) = 1 − t a n ( a ) t a n ( b ) t a n ( a ) + t a n ( b ) ,
t a n ( t a n − 1 ( x x − 3 ) + t a n − 1 ( x x − 4 )) = tan( 4 π )
1 − t a n ( t a n − 1 ( x x − 3 ) ) t a n ( t a n − 1 ( x x − 4 ) ) t a n ( t a n − 1 ( x x − 3 ) ) + t a n ( t a n − 1 ( x x − 4 ) ) =1 ,
resulting in a quadratic equation: \
1 − ( 1 − x 3 ) ( 1 − x 4 ) 1 − x 3 + 1 − x 4 = 1
whose solution is x = 6 , hence the area is A = 2 1 ∗ 2 x ∗ x = x 2 = 6 2 = 3 6
Since ∠ C A B = ∠ C B A , it follows that A C = B C . If we take △ N B C and rotate it clockwise by 9 0 ° about point C , side B C will completely overlap side A C , point B will end up in point A , and point N will end up in a point marked as E . Now, we have that:
∠ A C B = 9 0 ° → ∠ C A M = ∠ C B N = ∠ E A C = 4 5 ° → ∠ E A M = ∠ E A C + ∠ C A M = 9 0 ° .
△ E A M is a right triangle, and by Pythagorean Theorem: E M = E A 2 + A M 2 = 5 .
Now, △ C E M and △ C M N are congruent, because:
From this, it must be that: M N = E M = 5 . So:
A B = A M + M N + N B = 3 + 5 + 4 = 1 2
A C = B C = 2 A B
P = 2 A C 2 = 4 A B 2 = 3 6