$4n$ Cubes

Probability Level 3

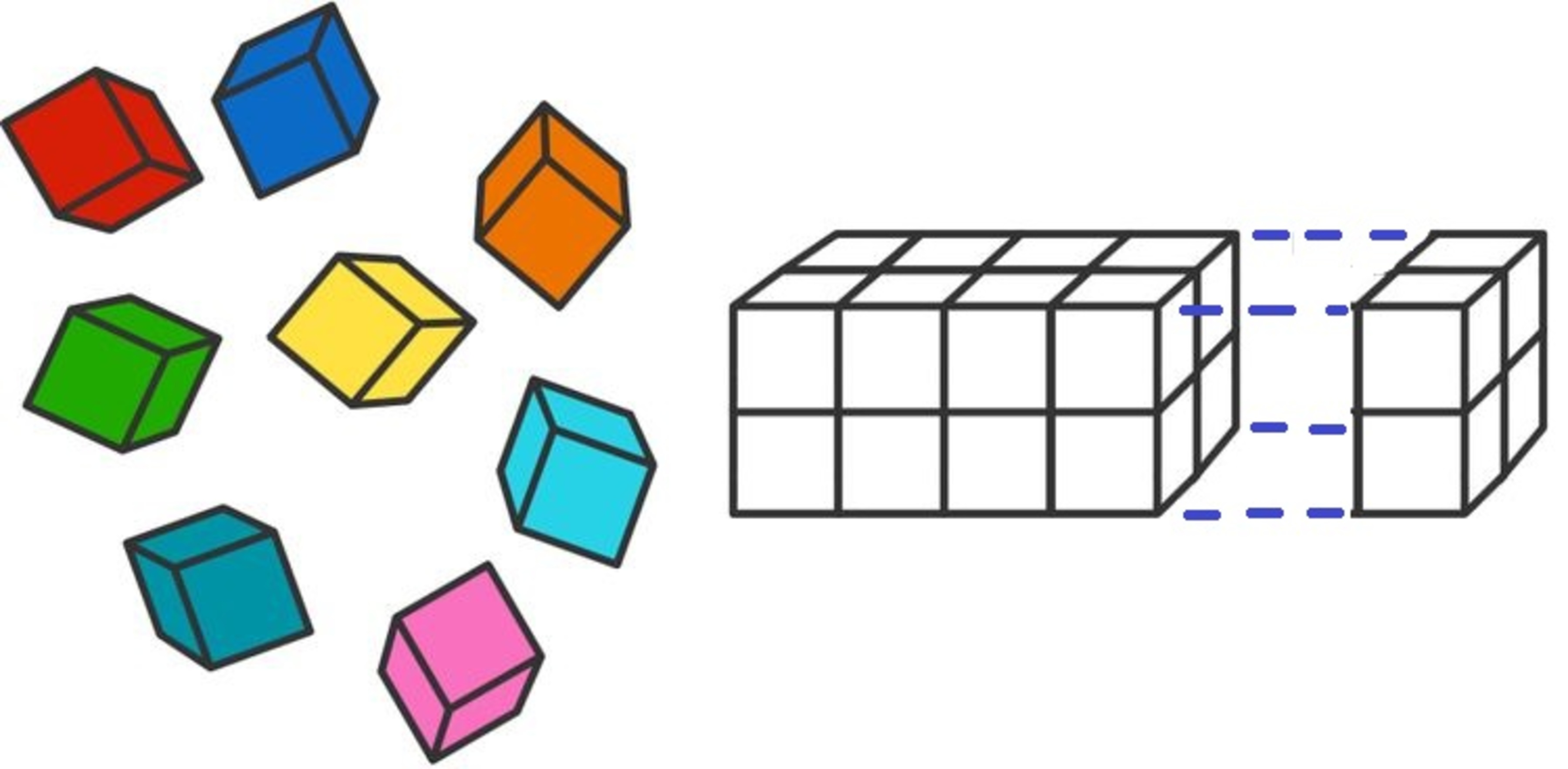
You have $4n$ cubes, $n>7$ , that can have eight different colors, and you arrange them into a $2 \times 2 \times n$ cuboid, so that no two cubes of the same color meet at a side, an edge or a vertex.

Lets take the colors to be - red, orange, yellow, green, blue, teal, cyan and magenta.

Given that the four cubes on one end are red, orange, yellow, and green, how many ways are there of coloring four cubes on the other end?

The answer is 24.

1 solution

Geoff Pilling
Nov 7, 2016

With this arrangement, every row of $2 \times 2$ cubes needs to necessarily contain different colors than the row before it. So, if we call the colors on one end $1$ , $2$ , $3$ , and $4$ . Then every other row must contain the colors $5$ , $6$ , $7$ , and $8$ .

So, if $n$ is odd, the four colors on the other end must be red, orange, yellow and green. If $n$ is even the four colors on the other end must be blue, teal, cyan and magenta.

Either way, you have four colors to paint on four cubes, so you have $4! = \boxed{24}$ ways to do this.

4 n 4n 4 n Cubes

The answer is 24.

1 solution

0 pending reports

$4n$ Cubes