4th Order RLC (3-20-2020)
An RLC circuit is excited by a DC voltage source V S . At time t = 0 , the inductors and capacitors are de-energized. The current flowing out of the source is I S . Define the cumulative energy supplied by the source as follows:
E S ( t ) = ∫ 0 t V S ( t ) I S ( t ) d t
Let I S m a x and I S m i n be the largest and smallest values of the source current over all time, respectively. Let E S m a x be the largest value of E S ( t ) over all time, and let E S ∞ be the limiting value of E S ( t ) as the elapsed time approaches infinity.
Determine the value of the quantity Q :
Q = I S m a x I S m i n E S ∞ E S m a x
Details and Assumptions:
1)
V
S
=
1
0
2)
R
1
=
R
2
=
L
1
=
L
2
=
C
1
=
C
2
=
1
3)
I
S
m
i
n
is negative. The other three quantities are positive
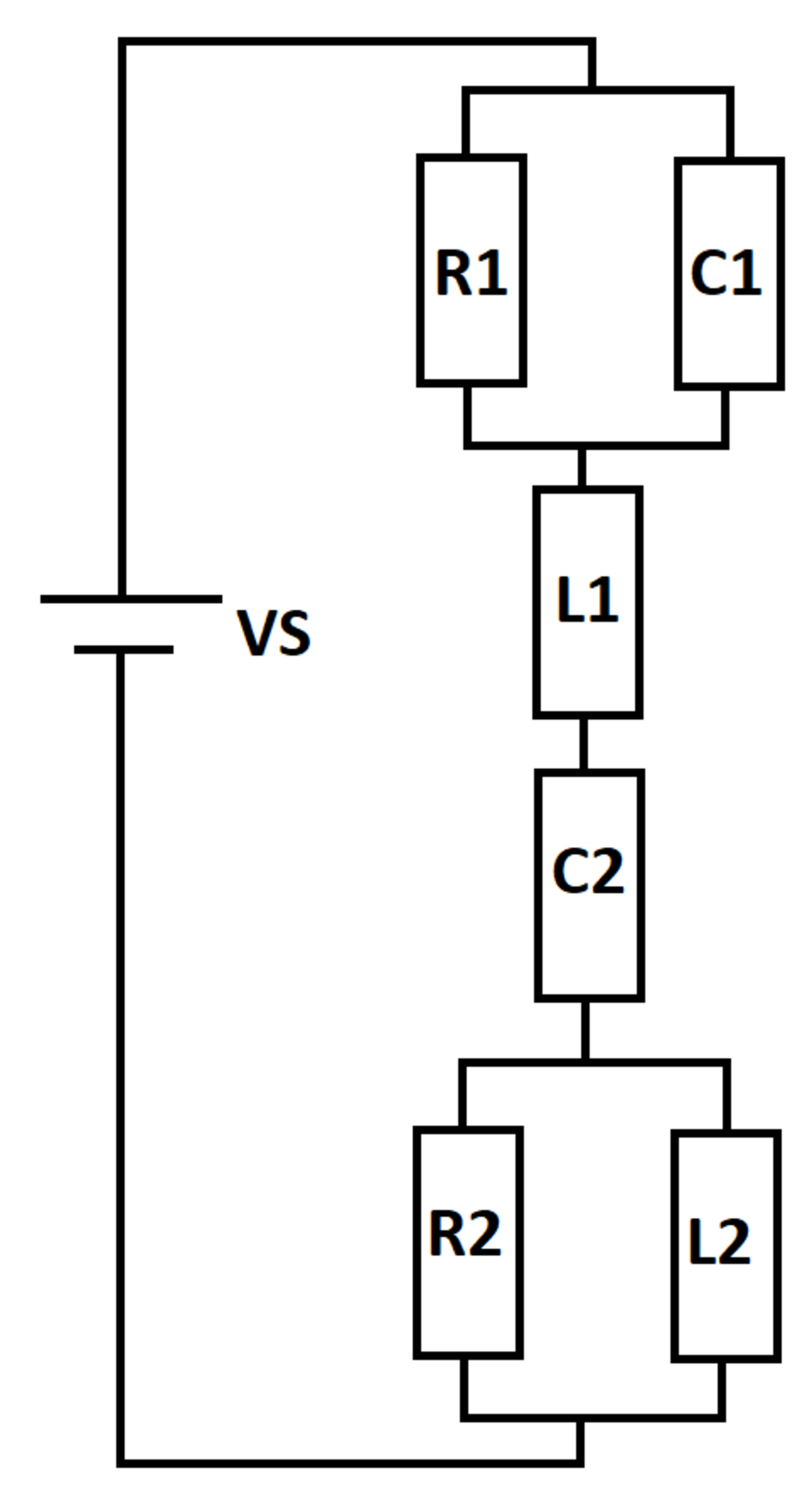
The answer is -5.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Guilherme Niedu How to do Laplace transformation?? Please
Log in to reply
@Neeraj Anand Badgujar it's an integral involving the function and an exponential. It has a lot of properties. It's better for you to read here: https://en.wikipedia.org/wiki/Laplace_transform
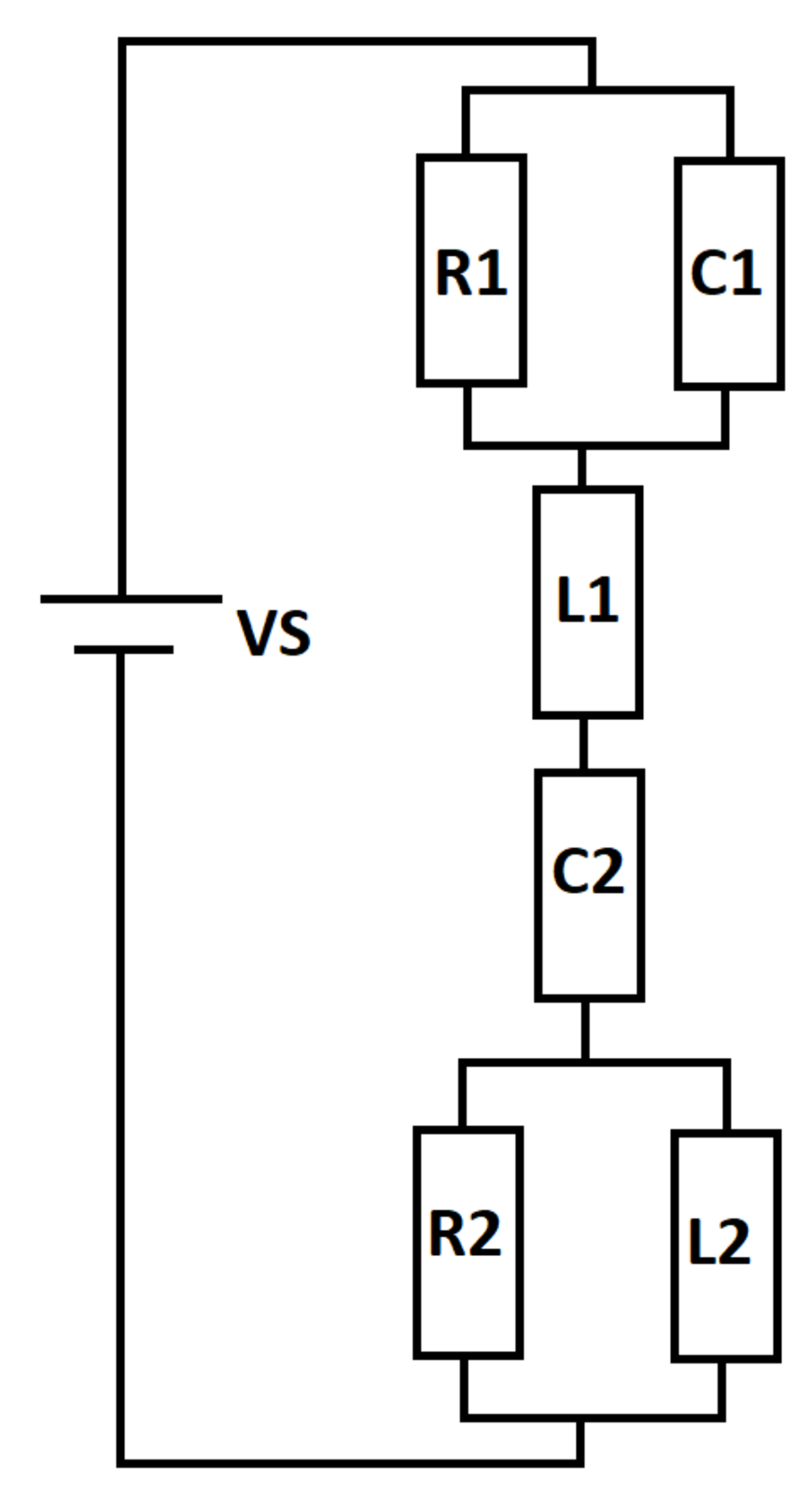
@Guilherme Niedu has given a very nice Laplace solution. I will show the state-space formulation that can be used in conjunction with numerical integration. Express the time derivatives of state variables ( V C 1 , V C 2 , I L 1 , I L 2 ) in terms of the state variables and the forcing function (the source). Once the solution routine is written, it is trivial to find energies, maximum quantities, etc.
For capacitor 1:
I R 1 = R 1 V C 1 I C 1 = I L 1 − I R 1 V ˙ C 1 = C 1 I C 1
For capacitor 2:
I C 2 = I L 1 V ˙ C 2 = C 2 I C 2
For inductor 1:
I R 2 = I L 1 − I L 2 V R 2 = R 2 I R 2 V L 1 = ( V S − V C 1 ) − ( V R 2 + V C 2 ) I ˙ L 1 = L 1 V L 1
For inductor 2:
V L 2 = V R 2 I ˙ L 2 = L 2 V L 2
Source Current:
I
S
=
I
L
1
Numerical integration (Euler, for example):
V C 1 ( k ) = V C 1 ( k − 1 ) + V ˙ C 1 ( k − 1 ) Δ t V C 2 ( k ) = V C 2 ( k − 1 ) + V ˙ C 2 ( k − 1 ) Δ t I L 1 ( k ) = I L 1 ( k − 1 ) + I ˙ L 1 ( k − 1 ) Δ t I L 2 ( k ) = I L 2 ( k − 1 ) + I ˙ L 2 ( k − 1 ) Δ t
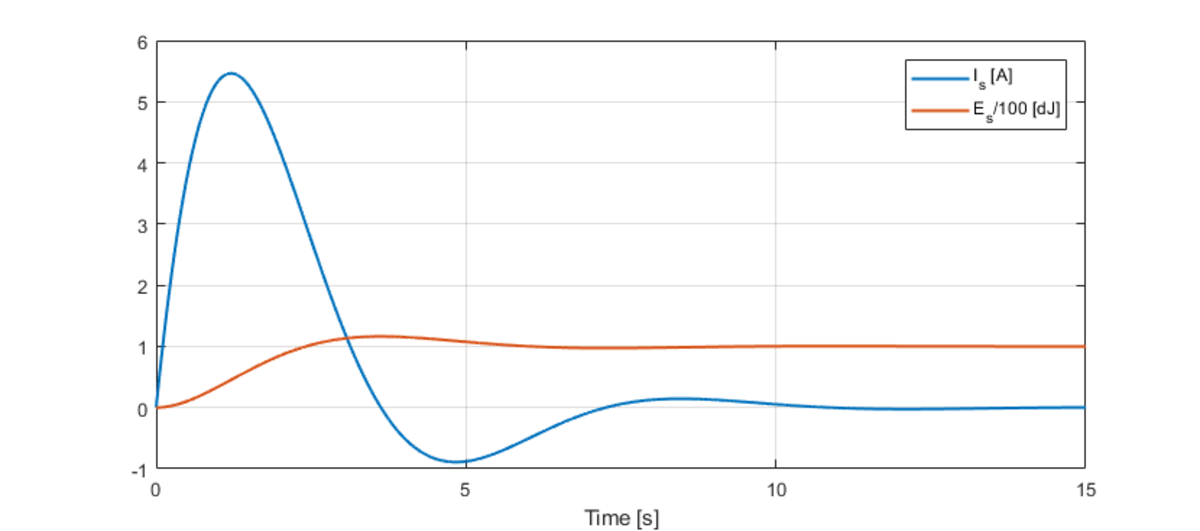
Just solved this one. Even I took a numerical route. The analytical solution posted by @Guilherme Niedu is impressive. Attached below is a plot showing the current and source energy variation with time.
Edited comment. The unit of energy shown in the plot is incorrect. It should have been hecto-joule [hJ] instead of deci-joule [dJ].
@Steven Chase
can you please provide me the code of your solution of this problem?
Thanks in advance
Let's use the impedances in the Laplace form. Since the ratio voltage-current in an inductor with indutance L is: V ( t ) = L d t d i ( t ) , in the laplace domain the ratio I ( s ) V ( s ) is L s . Likewise this ratio for a capacitor with capacitance C is C s 1 and for a resistor with resistance R is just R . So, the total impedance of this circuit is ( / / means impedances in parallel):
Z ( s ) = ( s 1 / / 1 ) + s + s 1 + ( s / / 1 )
Z ( s ) = s 1 + 1 s 1 ⋅ 1 + s + s 1 + s + 1 s ⋅ 1
Z ( s ) = s + 1 1 + s + s 1 + s + 1 s
Z ( s ) = s s 2 + s + 1
The current in the laplace domain will be:
I S ( s ) = Z ( s ) V S ( s )
Since the input voltage is a step of amplitude 1 0 , V S ( s ) = s 1 0 . So:
I S ( s ) = s 2 + s + 1 1 0
I S ( s ) = 3 2 0 ⋅ ( s + 2 1 ) 2 + 4 3 4 3
In the time domain:
I S ( t ) = 3 2 0 e − 2 t sin ( 2 t 3 )
Differentiating and making in equal to 0, one gets that the solutions are in the form:
tan ( 2 t 3 ) = 3
Or:
2 t 3 = 3 π + k π
t = 3 3 2 π ( 1 + 3 k )
Where k is an integer. Our maximum I S m a x occurs when k = 0 and our minimum I S m i n occurs when k = 1 . So:
I S m a x = 1 0 e − 3 3 π ≈ 5 . 4 6 2 9 3
I S m i n = − 1 0 e − 3 3 4 π ≈ − 0 . 8 9 0 6 4
Our quantity E s ( t ) will be:
E s ( t ) = 3 2 0 0 ∫ 0 t e − 2 t sin ( 2 t 3 ) d t
After integration by parts twice:
E s ( t ) = 1 0 0 − 3 2 0 0 e − 2 t sin ( 2 t 3 + 3 π )
Since the exponential will go to 0 as t goes to ∞ , it's easy to see that:
E S ∞ = 1 0 0
For E S m a x , differentiating and making it equal to 0 , one gets that the solutions are in the form:
tan ( 2 t 3 + 3 π ) = 3
Or:
2 t 3 + 3 π = 3 π + k π
t = 3 2 k π
At k = 0 we will actually have E S m i n = 0 , and E S m a x will be attained at k = 1 :
E S m a x = 1 0 0 ( 1 + e − 3 π ) ≈ 1 1 6 . 3 0 3 3 5
Calculating Q :
Q = − 1 0 0 ( 1 + e − 3 π ) e − 3 5 π ≈ − 5 . 6 5 8 7 5