5-12-13 and square!

Solution

I added Point G and H which is the same as E and F .

Point EF - Hypotenuse

FH=HE=17

45-45-90 triangle

EF= $7\sqrt { 2 }$

17(2) = $\boxed{34}$

Sorry for the bad edited image.

Let the intersection of $\overleftrightarrow { FD }$ and $\overleftrightarrow { EA }$ be $G$ and let the intersection of $\overleftrightarrow { EB }$ and $\overleftrightarrow { FC }$ be $H.$ By the converse of the Pythagorean theorem, $\angle AEB$ is a right angle. $\triangle CFD\cong \triangle AEB$ by $SSS$ and $\triangle DGA\cong \triangle AEB \cong \triangle BHC$ by $ASA$ . Therefore, $EGFH$ is a square with diagonal $EF$ . The side length of this square is $12+5=17$ , so the length of its diagonal is $17\sqrt { 2 }$ . $17*2$ = $\boxed {34}$

$I\quad used\quad a\quad coordinate\quad system\quad centered\quad at\quad C\quad and\quad \\ calculated\quad the\quad distances\\ using\quad the\quad Pythagorean\quad theorem\quad to\quad find\quad that\quad :\\ F(-\frac { 60 }{ 13 } \quad ;\quad \frac { 144 }{ 13 } )\quad and\quad E(\frac { 229 }{ 13 } \quad ;\quad \frac { 25 }{ 13 } )\quad .\\ Using\quad the\quad distance\quad formula\quad we\quad can\quad calculate\quad EF\quad .\\ EF\quad =\quad \sqrt { 578 } =\quad 17\sqrt { 2 } \\ \\ \therefore \quad a\quad =\quad 17\quad \& \quad b\quad =\quad 2\quad \\ \\ \boxed { ab=34 }$

First we notice that the angle $\angle FDC+ \angle FCD= 90 ^ \circ$ , knowing that, we now will construct triangles similars to $\triangle CDF$ and $\triangle ABE$ over the sides $AD$ and $BC$ (leaving the legs of this new triangles form continuous lines with the legs of the triangles $\triangle CDF$ and $\triangle ABE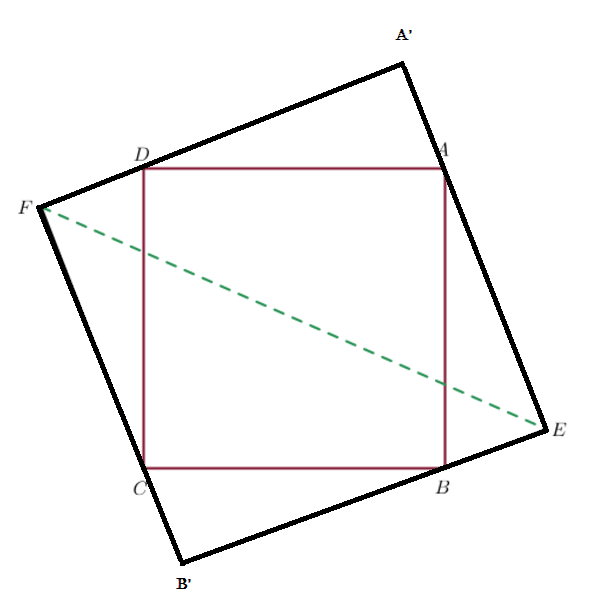$ ). It forms a square $A'EB'F$ with sides $5 + 12 = 17$ and the $EF$ asked it is the diagonal of $A'EB'F$ . $17^2 + 17^2 = EF^2\rightarrow EF=17\sqrt{2}\rightarrow a=17, b=2\Rightarrow \boxed{ab=34}$

Extend line $\overline{DF}$ to the lower left by $5 units$ . Call the end of the extension as point $P$

Making $\triangle{DPB}$ with sides $\overline{PB}$ parallel and equal to $\overline{FE}$

$\overline{DP} = 10$

$\overline{DB} = 13\sqrt{2}$

$\overline{PB} = \overline{FE}$

$\angle{BDP} = 45 + \cos^{-1} (\frac{5}{13})$

take cosine law

$(\overline{FE})^2 = (\overline{PB})^2 = 10^2 + (13\sqrt{2})^2 - 2(10)(13\sqrt{2})\cos [45 + \cos^{-1} (\frac{5}{13})]$

$\overline{FE} = 17\sqrt{2}$

$ab = 17 \times 2 = \boxed {34}$

EF² = (13 + 120/13)² + (2 (25/13) - 13)²=578 or EF = 17√2. Hence, ab = 17 (2 )= 34