5, 4, 3, 2, 1
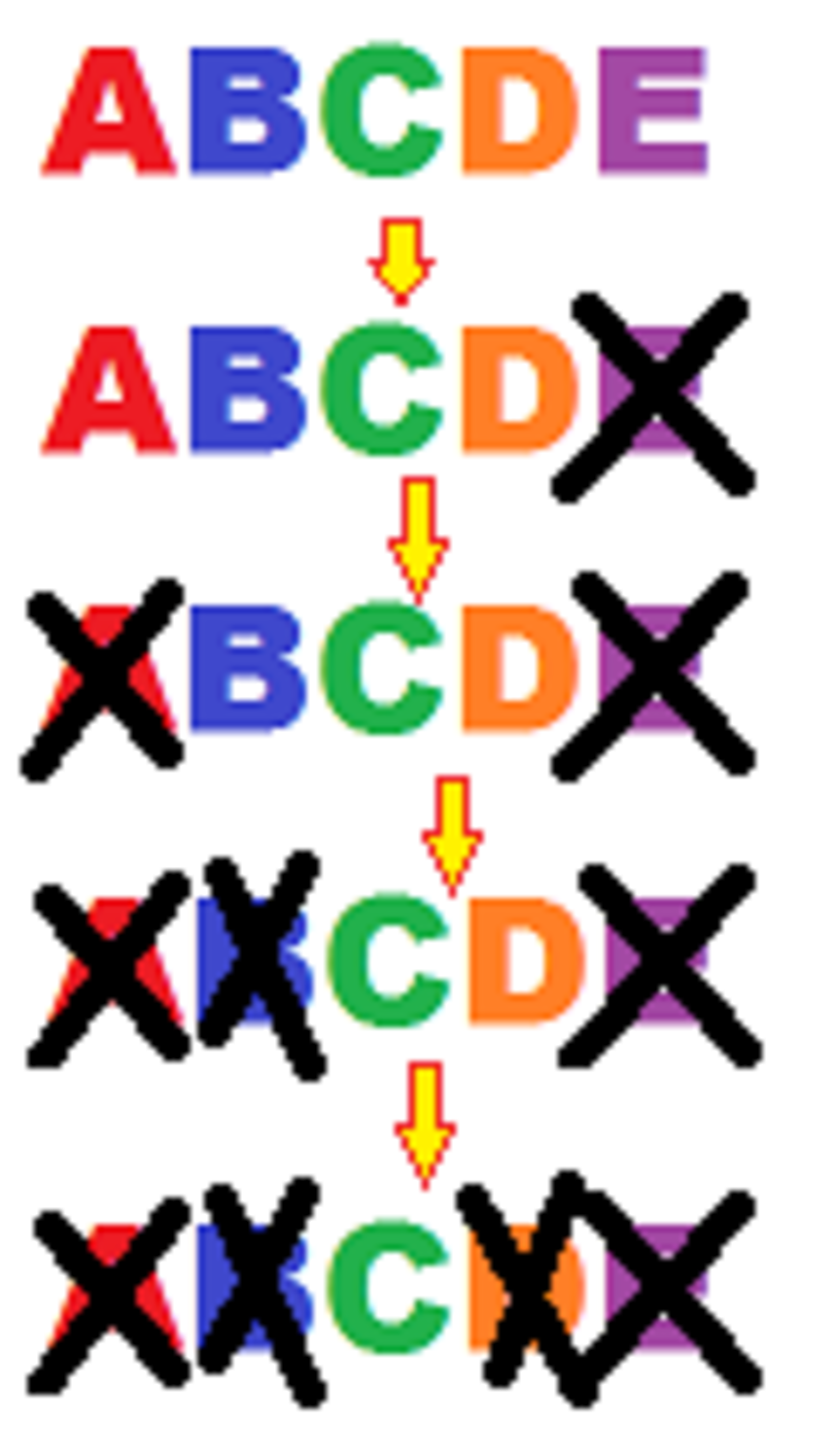
You start out with the string "ABCDE".
Every minute you randomly knock one letter off of the beginning or the end.
What is the probability that when there is one letter left it will be a C?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
After the first minute you will end up with C being second from one end.
So after 2 minutes, you have a 50% chance that C will be in the middle and 50% chance that it will be on the end.
If it is in the middle, then after one move it will be on the end and then on the last move have a 50% chance of being picked.
If it was on the end, it has a 50% chance of making it to the final 2, and then 50% chance of winning against the final two.
Therefore, the probability for having a "C" in the end is given by:
P = 2 1 ⋅ 2 1 + 2 1 ⋅ 4 1 = 8 3
Let's name the two operations, say F = removing front character and R = removing rear character.
So, total number of ways to keep last character is done by four operations.So number of ways is 2 4 = 1 6 .
Now to keep last character as C the following operations can be done
F → R → F → R F → F → R → R F → R → R → F
Now F can be replaced by R and we get again 3 methods.
So, total ways 3 + 3 = 6
So, the required probability is 1 6 6 = 8 3