5 Cans Together...
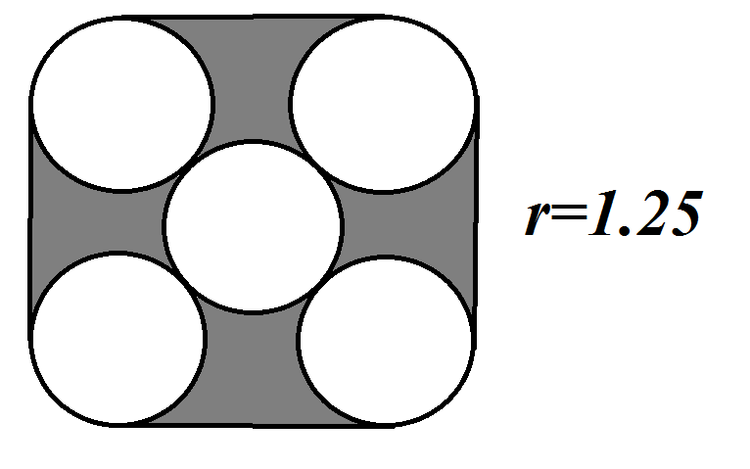 We have 5 cans of the same radius
, arranged as above, such that the centers of the 4 outer can form a square. If you put a string around them, can you find the area of the unoccupied portion (shaded area) of the cans?
We have 5 cans of the same radius
, arranged as above, such that the centers of the 4 outer can form a square. If you put a string around them, can you find the area of the unoccupied portion (shaded area) of the cans?
Details and Assumptions
The answer is in square units.
Round answers to 3 or more decimal places.
The answer is 10.54271544.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Image of the constructions i did here
I divided the shape up into 3 different shapes. First was a square, drawn by connecting the midpoints of the outer 4 circles. Then i drew lines from the center of each of the outer circles to where they are tangent with the perimeter.
Using special right triangles, one knows each side of the square is 2 . 5 2 , and the area of it would be ( 2 . 5 2 ) 2 .
Then we find the area of each of the identical outer rectangles, which have a length equal to that of the square , 2 . 5 2 , and a height equivalent to the radius, 1.25. The total area of the 4 rectangles would be 4 ( 2 . 5 2 ∗ 1 . 2 5 ) or 1 2 . 5 2 .
Finally, we have 4 quarter circles remaining, and their areas combines to make 1 . 2 5 2 π .
We add the 3 areas together, and subtract the 5 circles to get our final answer:
( 2 . 5 2 ) 2 + 1 2 . 5 2 + 1 . 2 5 2 π ) − 5 ( 1 . 2 5 2 π ) = 1 0 . 5 4 3