5 Circles and a Trapezoid
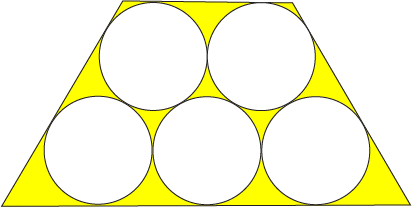 The figure to the right shows 5 unit circles that are tangent to each other and the edges of the trapezoid. If the yellow area can be expressed as
(such that
are integers and
is square-free), then find
.
The figure to the right shows 5 unit circles that are tangent to each other and the edges of the trapezoid. If the yellow area can be expressed as
(such that
are integers and
is square-free), then find
.
Note: I did not create this problem; I simply solved it and decided to post it on here. Credit goes to my math teacher.
The answer is 6.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of the yellow region A yellow is given by the area of the trapezoid A trapezoid minus the area of the 5 circles A circle .
From the figure, we note that the length of the base of the trapezoid a b = 4 + 2 a = 4 + tan 3 0 ∘ 2 = 4 + 2 3 . The length of its top a t = 2 + 2 b = 2 + 2 tan 3 0 ∘ = 2 + 3 2 . The height of the trapezoid h = 2 + c = 2 + 2 sin 6 0 ∘ = 2 + 3 .
Therefore, we have:
A yellow = A trapezoid − 5 A circle = 2 ( a b + a t ) h − 5 π 1 2 = 2 1 ( 4 + 2 3 + 2 + 3 2 ) ( 2 + 3 ) − 5 π = 1 0 + 3 1 7 − 5 π
Then d a + b + c = 5 1 0 + 1 7 + 3 = 6 .