5 Circles

Relevant wiki: Length and Area - Composite Figures

$\quad$

$\quad$

$\quad$

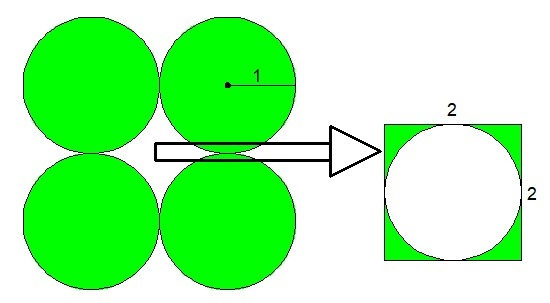
The figure is symmetrical about its midpoint,

so we can split it into 4 equal regions as shown above.

If we want to find the area of the entire region,

it is equivalent to 4 times the area of the figure below.

$\quad$

$\quad$

$\quad$

$\quad$

$\quad$

The area of the figure on the consists of a dark green circle and a light green region.

The area of the dark green circle is just the area of a unit circle, $\pi r^2 = \pi$ .

The area of the light green region is the area of a square with side length 1, minus the area of a quarter of a unit circle:

$1^2 - \dfrac14 \pi \cdot 1^2 = 1- \dfrac14\pi.$

Thus, the total area of the figure on the right is $\pi + \left( \dfrac14 - \dfrac14\pi\right) = 1 + \dfrac34\pi$ .

Multiply this number by 4 gives us the desired answer $\boxed{4+3\pi }$ .

$A=4\pi r^2+(2^2-\pi r^2)=4 \pi+4- \pi =$ $\boxed{4+ 3\pi}$

The radius of each of the outer circles is 1. So, if we connect the centers of each circle, we get a square that is 2 units x 2 units in dimension. This includes 1/4 of each circle, leaving the area of the remaining outer circle at 3/4 * π x 1², or 3π/4. Multiplying that by 4 circles, we get 4 x 3π/4=3π. Adding this to the square, we get the total green area to be (2x2)+3π; or 3π+4 ☺☺☺☺

If we draw a 2 × 2 square around any circle (other than the middle one; one of its vertices is at the center of the "middle" circle), we will see the green area within this square is (the area of the circle + a quarter of the area outside the circle (the difference of the areas of the square and the circle)):

$a = π + \frac {1}{4} (2^2 - π) =\frac {3}{4} π + 1$

As we have 4 "outer" circles, each with a 2 × 2 square around it:

$A = 4a =4 × ( \frac {3}{4} π + 1) = \boxed {4 + 3π}$