5 circs in a hex

Geometry Level 4

Five unit circles are packed inside the smallest possible regular hexagon. What is the side length of the hexagon?

Slightly less than 3 Exactly 3 Slightly greater than 3

Jeremy Galvagni by Jeremy Galvagni , 48, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Geoff Pilling
Nov 15, 2018

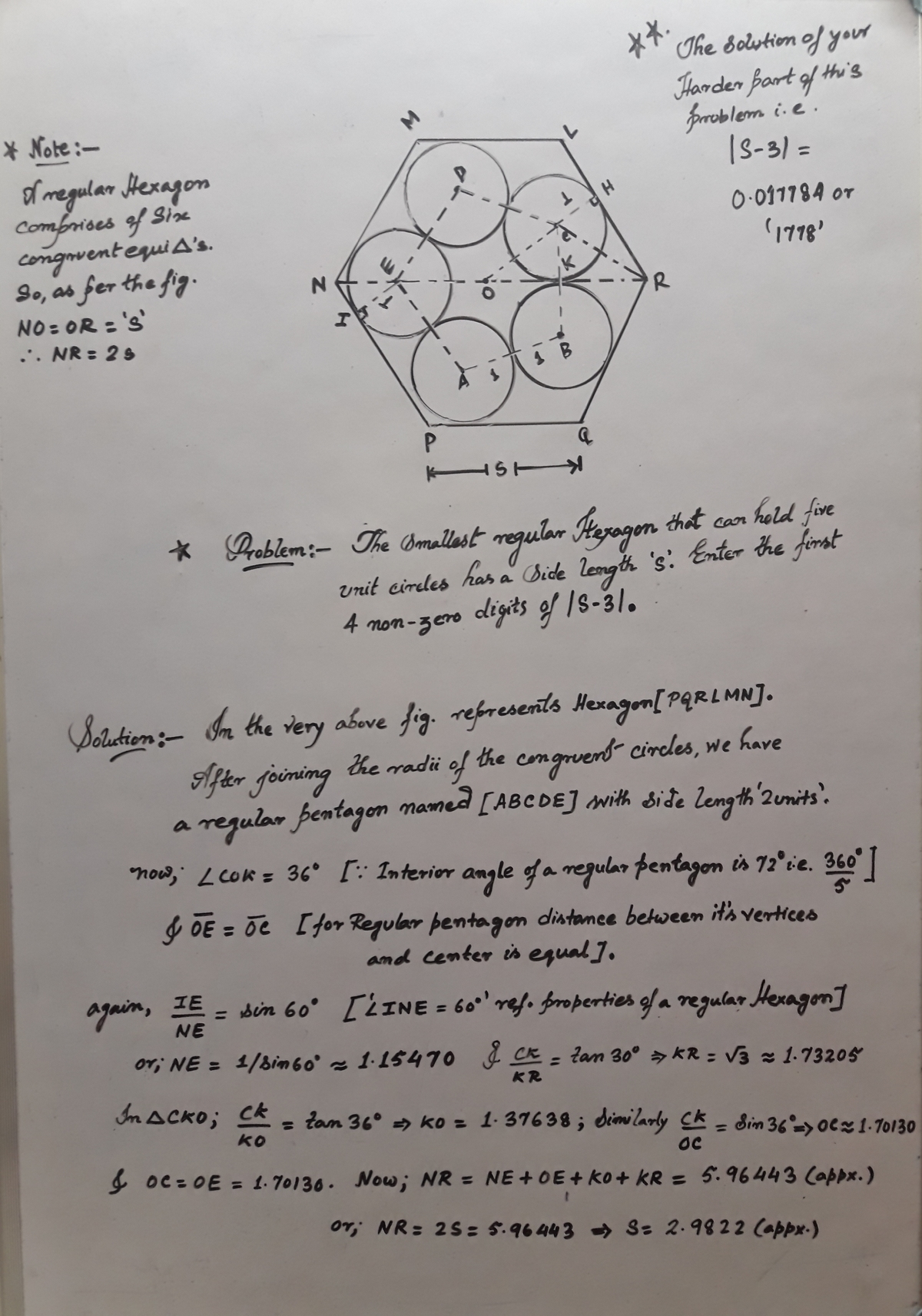
The side length with six unit circles would be exactly three. For five, clearly you can optimize a bit, making the radius of each circle slightly bigger for the same sized hexagon, meaning that the relative dimension of the hexagon side would be slightly less than 3.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

I'm embarrassed I didn't think of this. Probably because I was more intent on finding the exact solution. This problem was an afterthought to have an easier version.

Jeremy Galvagni - 2 years, 6 months ago

Log in to reply

That's funny... By the wording of your answers I figured this was the kind of solution you were aiming for... Given that it can be solved with this type of intuition I figured it was a pretty cool problem! 😎

Geoff Pilling - 2 years, 6 months ago

I take back my embarrassment. The side length for 6 circles is not exactly 3.

Jeremy Galvagni - 2 years, 6 months ago

Log in to reply

Ooooooops... 🤔

Geoff Pilling - 2 years, 6 months ago
Nibedan Mukherjee
Nov 15, 2018

1 Helpful 0 Interesting 0 Brilliant 0 Confused

In the correct optimal solution, the pentagon is not regular.

In your answer above, the circles centered at A and D will not be completely contained within the hexagon.

Jeremy Galvagni - 2 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...