5 Olympic rings
Geometry
Level
4
Five unit circles are inscribed in a semicircle in a symmetrical way, as shown.
Find the radius of the semicircle.
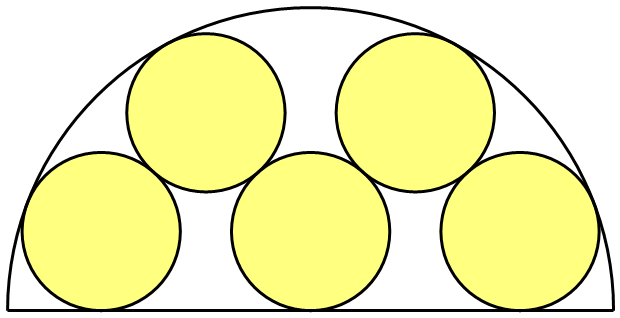
The answer is 3.828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's put another unit circle on top of the existing circles as shown below: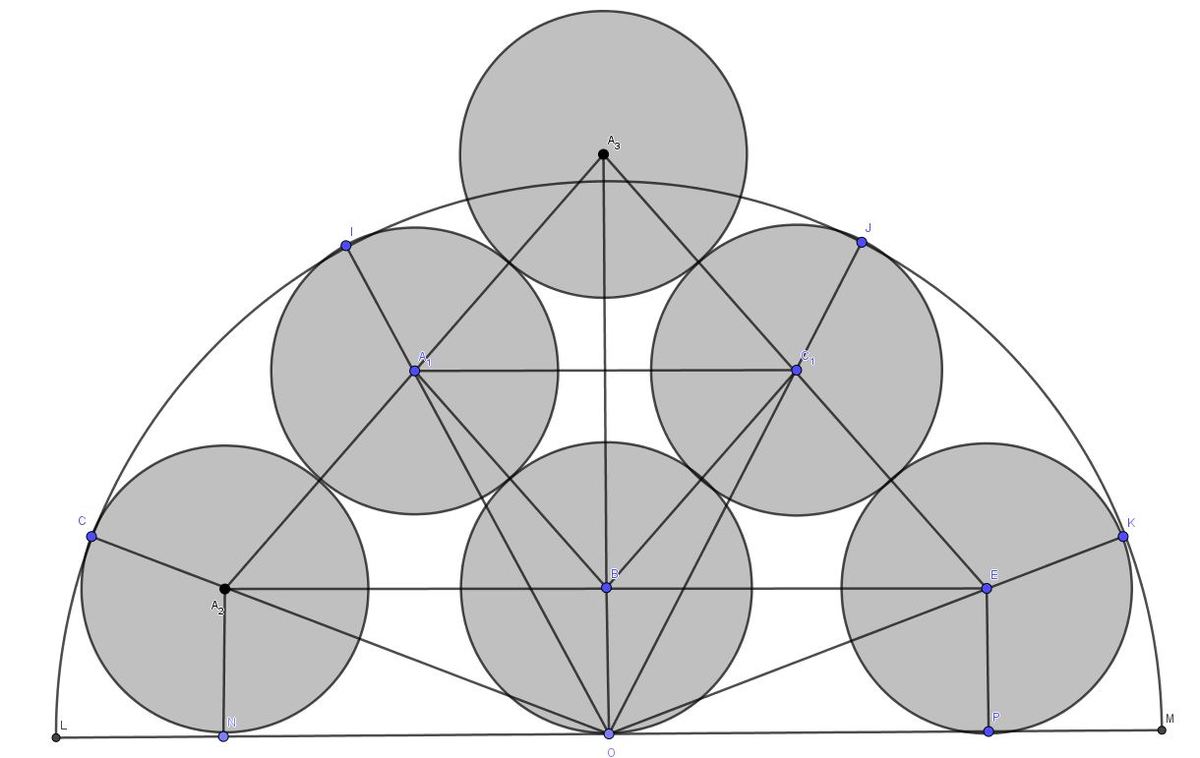
∠ E O P = α ⇒ ∣ O E ∣ = sin α 1 = ∣ O C 1 ∣ = ∣ O A 1 ∣ = ∣ O A 2 ∣ .
∠ C 1 O E = 2 α ⇒ ∠ O E A 3 = ∠ A 3 O E = 9 0 ∘ − α ⇒ ∠ O A 3 E = 2 α .
A 1 A 3 C 1 B is parallelepiped, so ∠ A 3 B C 1 should be 2 α .
Solution 1: ⇒ ∠ A 1 B C 1 = 4 α , ∠ A 1 O C 1 = 1 8 0 ∘ − 6 α
Cosine rule for finding trianlge sides: ∣ A 1 C 1 ∣ = x
∣ A 1 C 1 ∣ 2 = ∣ A 1 B ∣ 2 + ∣ C 1 B ∣ 2 − 2 ⋅ ∣ A 1 B ∣ ⋅ ∣ C 1 B ∣ ⋅ cos 4 α ⇒ x 2 = 2 2 + 2 2 − 2 ⋅ 2 ⋅ 2 ⋅ cos 4 α ⇒ x 2 = 8 ⋅ ( 1 − cos 4 α )
∣ A 1 C 1 ∣ 2 = ∣ O A 1 ∣ 2 + ∣ O C 1 ∣ 2 − 2 ⋅ ∣ O A 1 ∣ ⋅ ∣ O C 1 ∣ ⋅ cos ( 1 8 0 ∘ − 6 α ) ⇒ x 2 = ( sin α 1 ) 2 + ( sin α 1 ) 2 − 2 ⋅ sin α 1 ⋅ sin α 1 ⋅ cos ( 1 8 0 ∘ − 6 α ) = sin 2 α 2 ⋅ ( 1 + cos 6 α )
⇒ x 2 = 8 ⋅ ( 1 − cos 4 α ) = sin 2 α 2 ⋅ ( 1 + cos 6 α ) = 1 − cos 2 α 4 ⋅ ( 1 + cos 6 α ) ⇒ 2 ⋅ ( 1 − cos 4 α ) ⋅ ( 1 − cos 2 α ) = 1 + cos 6 α
cos 4 α = 2 cos 2 2 α − 1 ; cos 6 α = 4 cos 3 2 α − 3 cos 2 α
( cos 2 α = a ) : ⇒ 2 ( 2 − 2 a 2 ) ( 1 − a ) = 1 + 4 a 3 − 3 a ⇒ 4 a 2 + a − 3 = 0 ⇒ ( a + 1 ) ( 4 a − 3 ) = 0 ⇒ a = 4 3 .
c o s 2 α = 4 3 = 1 − sin 2 α ⇒ sin α = 8 1 ⇒ ∣ O E ∣ = sin α 1 = 8 . ⇒ R = ∣ O K ∣ = ∣ O E ∣ + ∣ E K ∣ ⇒ R = 8 + 1 ≈ 3 . 8 2 8
Solution 2: I later realized the easiest way to find the value of sin α .
△ O A 3 E ∼ △ E O C 1 ⇒ ∣ O C 1 ∣ ∣ A 3 E ∣ = ∣ E C 1 ∣ ∣ O E ∣ ⇒ 4 sin α 1 = sin α 1 2 ⇒ sin α 1 = 8 = ∣ O E ∣ = ∣ O C 1 ∣ ⇒ R = ∣ O E ∣ + ∣ E K ∣ = 8 + 1 ≈ 3 . 8 2 8