5 Squares
The above is one possible way to arrange 5 unit squares into a polygon, and this polygon has a perimeter of 12. What is the minimum possible perimeter of a polygon that can be constructed with 5 unit squares?
Details and Assumptions:
- No overlapping is allowed.
- A vertex can only touch a vertex--not anywhere on the side--of other squares.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Thanks for your solution. This problem was inspired by this paper .
@Challenge Master note:
Interesting... I had two other possibilities in mind:
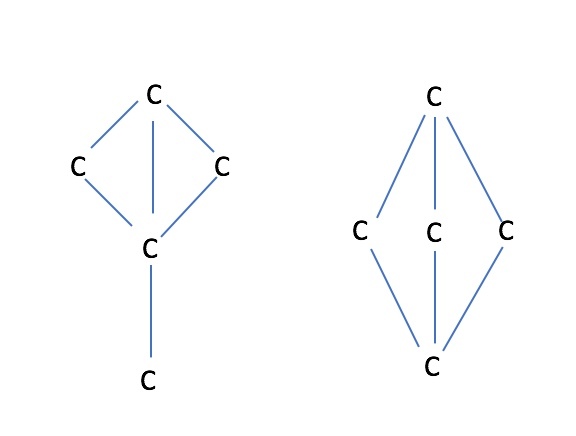
Log in to reply
Hm, I haven't seen either one of these before. The first one is 1-methyl-bicyclo[1.1.0]butane?
I thought of hydrocarbons straight away! Cylic alkanes have fewer hydrogens:)
It is easily to find for the perfect square number of unit squares with minimum possible perimeter.
1 unit square(1x1 grid)-> 1.4=4, 4 unit square(2x2 grid)->2.4=8, 9 unit square(3x3 grid)->3.4=12..etc
For 4 unit squares, the minimum possible perimeter is 8. If we add the fifth one with the existing 4 (2x2 grid)we will get the polygon with minimum perimeter 10.
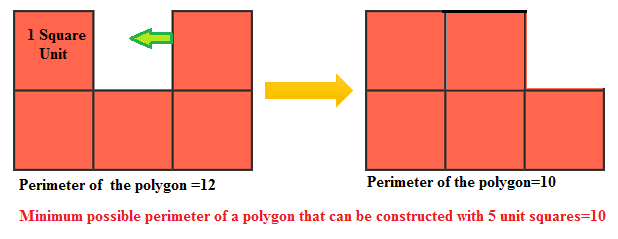
How do you know there is no configuration with smaller perimeter?
Log in to reply
We can easily find minimum for the number of perfect square unit squares with minimum possible perimeter.
1 unit square(1x1 grid)-> 1.4=4, 4 unit square(2x2 grid)->2.4=8, 9 unit square(3x3 grid)->3.4=12..etc
For 4 unit squares, the minimum possible perimeter is 8. If we add the fifth one with the existing 4 (2x2 grid)we will get the polygon with minimum perimeter 10.
I get it now. Thanks for the solution. I didn't think 💭 of that in the first place
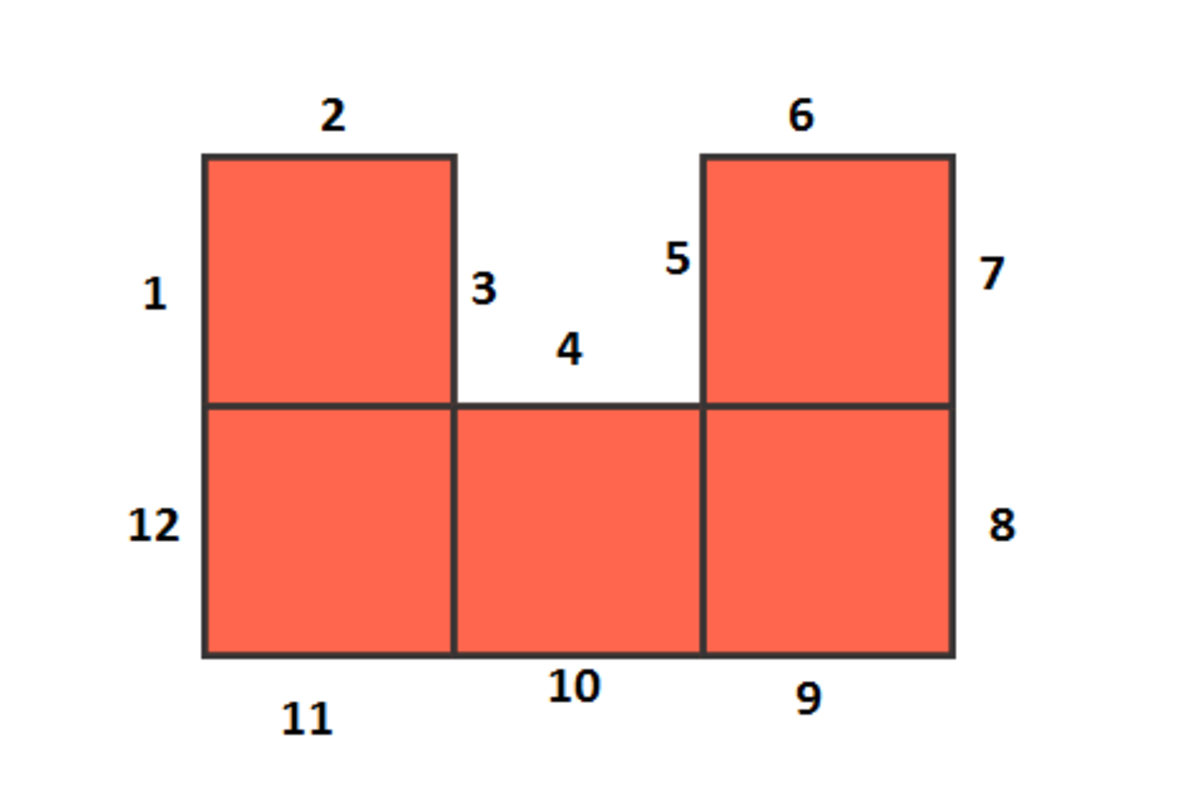
Observe that the perimeter of each configuration of squares attached side by side is EVEN. Reason: The perimeter breaks down in horizontal and vertical steps. In each of these two directions, the number of 'forward' steps equals the number of 'backward' steps. Hence, each is even, and so is their sum.
This eliminates 9 and 11.
A 2 × 2 square has perimeter 8, which is least among all 4-square configurations. Hence, 5-square configurations will have a perimeter at least 10. The P-pentomino is such a configuration.
That's a great way to eliminate the odd options! And I was thinking for such a long time on whether we can do better than 10 or not...
We'll have to get as many squares to touch each other as possible. Actually, we'll just have to limit the number of "free" sides, which count for the perimeter... Thus we form a square of side 2, and add one little square where we want to get a result of, which is the actual minimum
I see, that saved a lot of trials and errors!
We can simplify this by thinking of the fact that in such a polygon, each square can have 1,2, or 3 sides on the perimeter. So what shape can we make that minimizes 3-sides-on-perimeter squares? The answer is a square 2x2 with one square sticking out
Agree, this is a nice reasoning.
The number of arrangements for 'n' number of squares to form a polygon according to the given conditions, satisfies fibonacci criteria ie. F(n) = F(n-1) + F(n-2). Hence we can draw arrangements for n=1 (number of squares) then n=2 and using these we can easily draw different possible arrangements for n=3,4,5 and as we already know how many arrangements are there (1 1 2 3 5).After that, it is trivial task to calculate the perimeter.
PS: For n=1 --> 1 n=2 --> 1 n=3 --> 2 n=4 --> 3 n=5 --> 5
Don't consider symmetric arrangements as different arrangements ie. if the given the figure had the middle element missing in the bottom row instead, it would have been similar to the one above, so count them as 1.
PSS---> To draw different arrangements.Consider we are drawing for n=4 and we have arrangements for n=3, then for each arrangement of n=3, try placing a box at each edge and see if it is a different arrangement from the ones you have drawn till now.If yes, then count it as separate arangement and continue this process until you have 3 arrangements (as F(4)=3).
Why is the number of arrangements for n number of squares to form a polygon satisfies the Fibonacci criteria?
Since they are squares they have
equal lenghts
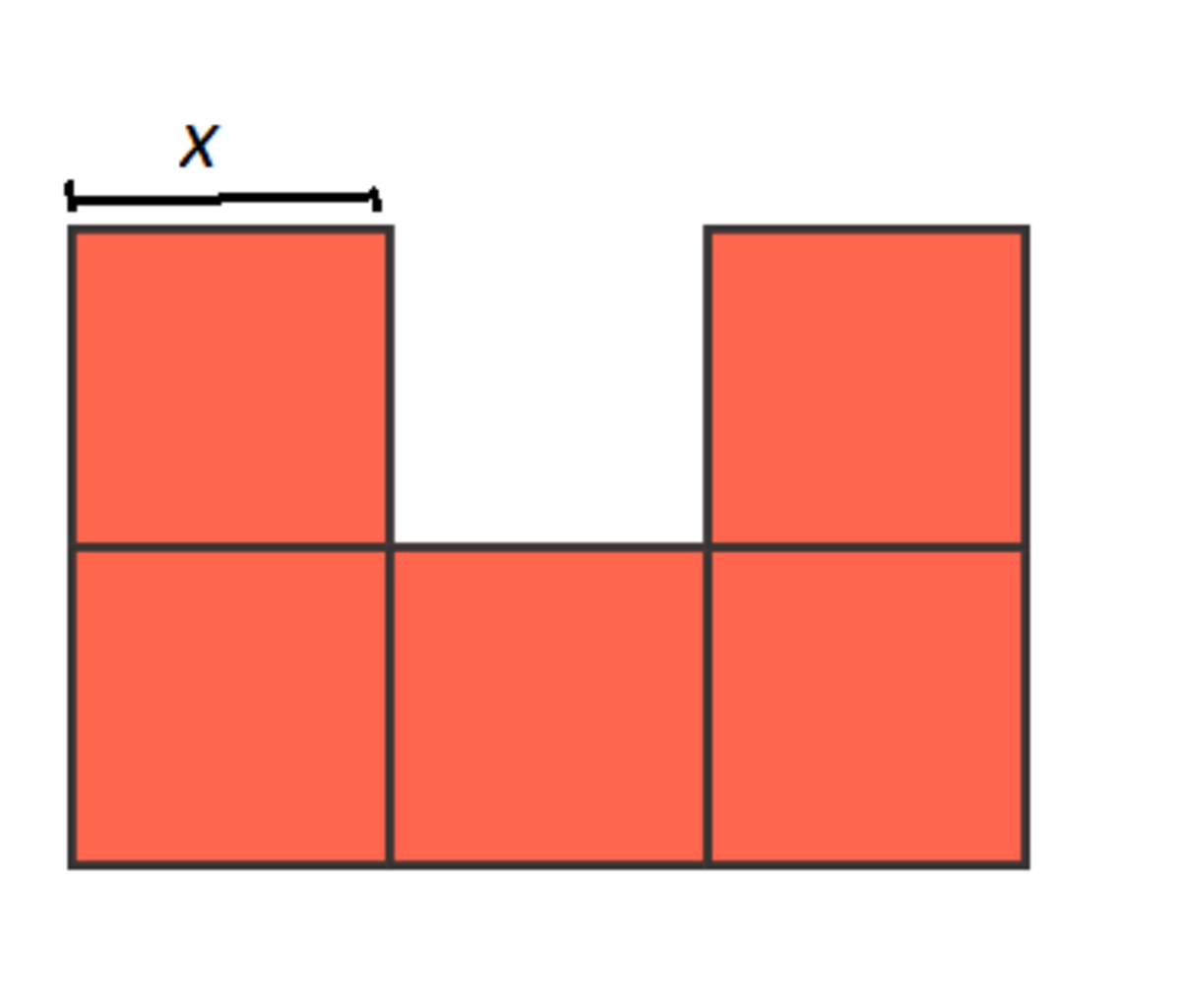
so we end with the equation 1 2 x = 1 2
x=1
When they are the closest possible the perimeter its minor, since the squares will tangentiate, re arranging the squares while following this logic we end up with:
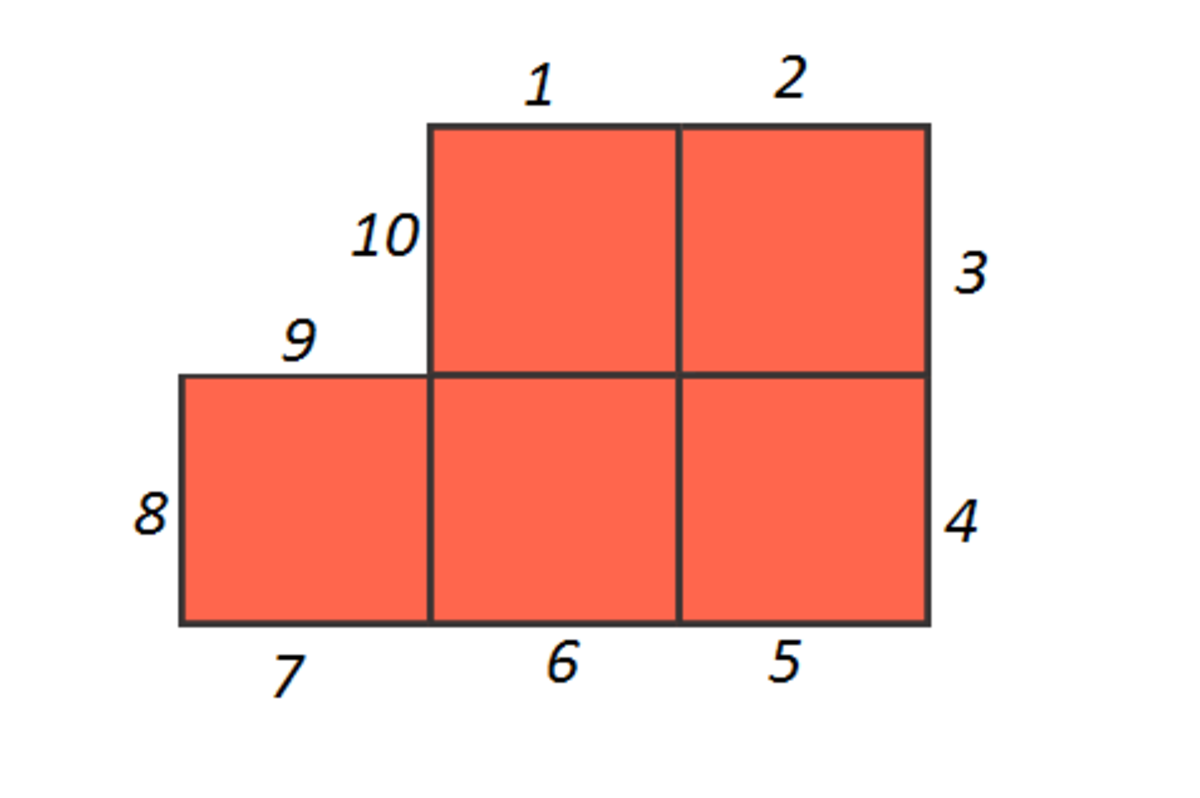
So awnser is 10
This is my final configuration as well, but how do you know that there isn't any configuration that produces lesser perimeter?
Log in to reply
because like i said they're the closest possible
When left separate, the squares have a total perimeter of 5 × 4 = 2 0 . For every connection we make, this number decreases by 2. Thus we try to optimize the number of connections.
Several of the shapes can be built as follows: (1) Start with a square. (2) Add the next square, connecting it to the first one. (3) Add the third square, connecting it to one existing square. (4, 5) Etc. In this way there will always be four connections, and therefore a perimeter of 2 0 − 4 × 2 = 1 2 .
□ ∣ □ − □ − □ ∣ □
To improve this, at some point we must add a square that can be connected to two existing squares. In other words, it must complete a "loop".
□ ∣ □ − − □ ∣ □ − □
Since this adds an extra connection, the perimeter is now only 2 0 − 5 × 2 = 1 0 .
Improving this would require building a second loop. This is clearly impossible with only five squares.
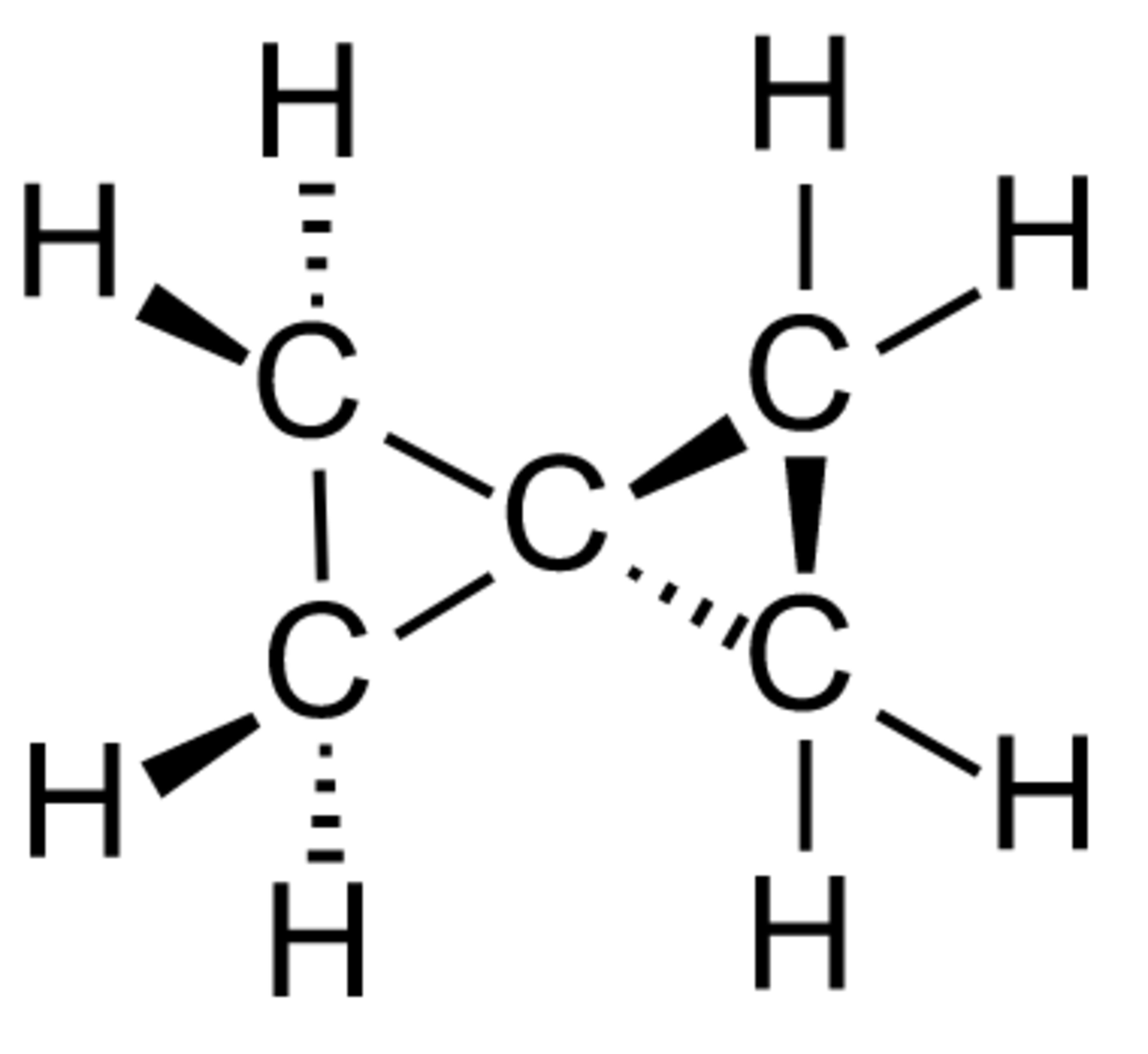
Note : This problem is somewhat related to building hydrocarbons in organic chemistry: the squares are like carbon atoms, and the perimeter is the number of hydrogen atoms. Of course, the square "grid" of this problem limits the number of possibilities; in chemistry one can build a C 5 H 8 molecule with two rings, using bonding angles less than 90 degrees.