5-Stage Pipeline
Computer Science
Level
3
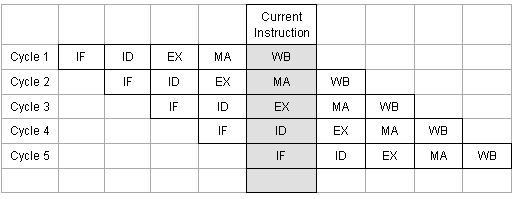
Determine how many clock cycles a basic 5-stage pipeline requires in order to complete a 10-instruction program.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Instruction pipelining is a technique that allows faster CPU throughput, that is the number of instructions that can be executed in a unit of time. Each instruction is split up such that instructions can be executed in parallel and can be processed concurrently, rather than processing each instruction sequentially. In an ideal pipeline architecture, the execution of the first instruction requires as many clock cycles as how many stages there are, but the second instruction will be completed only after one additional cycle, as well as every following instruction. One can deduce that the number of clock cycles T k with this pipeline technology is T k = k + ( n − 1 ) , where k is the number of this pipeline's stages and n is the number of instructions of the program considered. Therefore, T k = 5 + ( 1 0 − 1 ) = 5 + 9 = 1 4 .